Cho hàm số f(x)= x(x+1)(x+2) (x+3)... (x+2019).
Tính f'(0)
A. 2018!
B. 2019!
C. 0
D. 1
Những câu hỏi liên quan
cho hàm số f(x)=ax2+bx+c ( x là ẩn , a,b,c là hệ số ) . Biết rằng f(0)=2018, f(1)=2019,f(-1)=2017 . Tính f(-2019)
cho hàm số f(x)=9^x/9^x+3.Tính f(1/2019)+f(2/2019)+f(3/2019)+.....+f(2018/2019)
bài này không khó nghe em chẳng qua là nó hơi dài
em phải nhớ công thức tính tổng của dãy số, công thức tổng quát ấy là n.(a1+an)/2 (n là số số hạng, a1 là phần tử thứ nhất và an là phần tử thứ n)
số số hạng thì dễ rồi đúng k
còn a1+an là bằng f(1/2019)+f(2018/2019)
em thế f(1/2019) vào f(x) cái kia cũng vậy
xong em chịu khó nhân vào có dạng là a^n.a^m
vậy là ra thôi em
Đúng 0
Bình luận (0)
Cho hàm số yf(x)x(x+1)(x+2)(x+3)...(x+2018)(x+2019). Tínhf’(0). A. 0. B.
2019
1
+
2019
2
C.
P
2019
D. 2019
Đọc tiếp
Cho hàm số y=f(x)=x(x+1)(x+2)(x+3)...(x+2018)(x+2019). Tínhf’(0).
A. 0.
B. 2019 1 + 2019 2
C. P 2019
D. 2019
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
-
1
(
a
,
b
∈
ℝ
)
. Đồ thị của hàm số yf(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 0 là: A. 4 B. 0 C. 3 D. 2
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
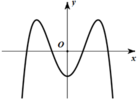
A. 4
B. 0
C. 3
D. 2
Cho hàm số yf(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)0 và thỏa mãn
f
(
x
)
2018
1
-
f
(
x
)
2
x
(...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R có đạo hàm cấp 3 với f’’’(x)=0 và thỏa mãn f ( x ) ' 2018 1 - f ' ' ( x ) = 2 x ( x + 1 ) 2 ( x - 2018 ) 2019 : f ' ' ( x ) , ∀ x ∈ R Hàm số g ( x ) = f ' ( x ) 2019 1 - f ' ' ( x ) có bao nhiêu điểm cực trị?
A. 1
B.2
C.3
D. 4
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra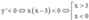 
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)(1-x)(x+2).g(x) + 2018 trong đó g(x)0, mọi x thuộc R. Hàm số yf(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Đọc tiếp
Cho hàm số y=f(x) xác định trên R và có đạo hàm f‘(x) thỏa mãn f’(x)=(1-x)(x+2).g(x) + 2018 trong đó g(x)<0, mọi x thuộc R. Hàm số y=f(1-x)+2018x+2019 nghịch biến trên khoảng nào?
Cho đa thức f(x)=ax\(^2\) +bx+c Biết f(1)=f(-1)=0 Tính M= a^2019+b^2019+c^2019+2018
Ta có :
\(f\left(x\right)=ax^2+bx+c\)
\(\Rightarrow\hept{\begin{cases}f\left(1\right)=a.1^2+b.1+c\\f\left(-1\right)=a.\left(-1\right)^2+b.\left(-1\right)+c\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}f\left(1\right)=a+b+c\\f\left(-1\right)=a-b+c\end{cases}}\)
mà \(f\left(1\right)=f\left(-1\right)\Rightarrow a+b+c=a-b+c\)
\(\Rightarrow b=-b\)
Đến bước này em không biết vì em học lớp 7
Đúng 0
Bình luận (0)
Từ \(b=-b\Rightarrow2b=0\Rightarrow b=0\)
\(\Rightarrow a+c=0\left(f\left(1\right)=0,b=0\right)\)
\(\Rightarrow a=-c\)
Thay \(b=0,a=-c\)vào biểu thức M ta được:
\(M=\left(-c\right)^{2019}+0^{2019}+c^{2019}+2018\)
\(=-c^{2019}+0+c^{2019}+2018\)
\(=\left(-c^{2019}+c^{2019}\right)+2018\)
\(=0+2018=2018\)
Vậy giá trị biểu thức M là \(2018\)
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f(x) thỏa mãn
f
(
x
)
(
1
-
x
)
(
x
+
2
)
g
(
x
)
+
2018
với
g
(
x
)
0
,
∀
x
∈
R
. Hàm số
y
f
(...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây?
A . ( 1 ; + ∞ ) .
B . ( 0 ; 3 ) .
C . ( - ∞ ; 3 ) .
D . ( 4 ; + ∞ ) .
