Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình log x - 20 + log 40 - x < 2
A. 19
B. 18
C. 10
D. 20
Đáp án B
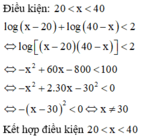
và x nguyên dương, vậy có 18 giá trị của x thỏa mãn đề bài.
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây : log x - 40 + log 60 - x < 2 ?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
P T ⇔ log x - 40 60 - x < 2 ⇔ x - 40 60 - x < 100 ⇔ x 2 - 100 x + 2500 > 0 ⇔ x - 50 2 > 0 ⇔ x ≠ 50 .
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 > 2 2 x
A. 4
B. 5
C. 2
D. 3
Ta có:
8 x . 2 1 - x 2 > 2 2 x ⇔ 2 3 x + 1 - x 2 > 2 x ⇔ 3 x + 1 - x 2 > x ⇔ x 2 - 2 x - 1 < 0 ⇔ 1 - 2 < x < 1 + 2
Mà x ∈ ℝ ⇒ x ∈ 1 ; 2 . Bất phương trình đã cho có 2 nghiệm nguyên dương.
Chọn đáp án C.
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 > 2 2 x
A. 4
B. 5
C. 2
D. 3
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 ≥ ( 2 ) 2
A. 4
B. 5
C. 2
D. 3
Cho hai số thực dương x, y thỏa mãn log x + log y ≥ log ( x 3 + 2 y ) Giá trị nhỏ nhất của P = 25x + y là
A. 375/4
B. 45/2
C. 195/2
D. 14 26
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 1 + log 5 x 2 + 1 ≥ log 5 m x 2 + 4 x + m thỏa mãn với mọi x ∈ R
A. 3
B. 6
C. 1
D. 7
