Cho hàm số y = f x có đồ thị như hình vẽ:
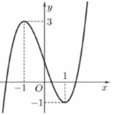
Số nghiệm của phương trình 4 f (x) + 3 = 0 là
A. 3.
B. 0.
C. 1.
D. 2.
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên
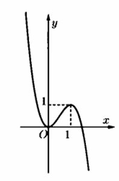
Tìm số nghiệm của phương trình f(x) = x
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f(x) có đồ thị như hình vẽ.
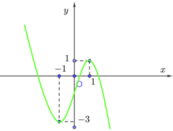
Số nghiệm của phương trình ![]() là
là
A. 3
B.5
C. 4
D. 6
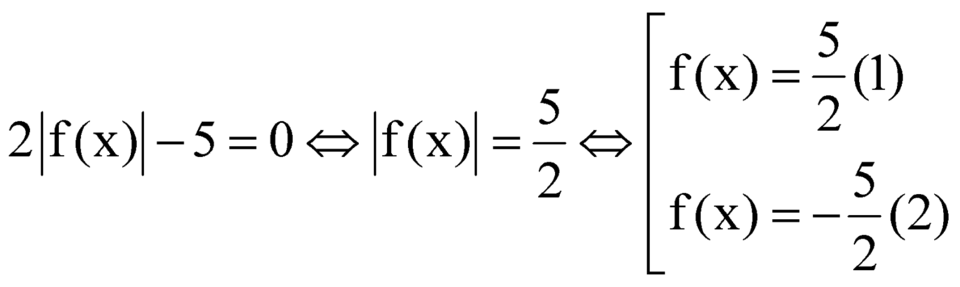
Số nghiệm của phương trình đã cho là tổng số nghiệm của phương trình (1) và phương trình (2).
Số nghiệm của phương trình đã cho là số giao điểm của đường thẳng ![]() và đường thẳng
và đường thẳng ![]() với đồ thị hàm số
với đồ thị hàm số![]()
Như vậy, dựa vào đồ thị hàm số ta thấy phương trình đã cho có 4 nghiệm.
Chọn C.
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2|f(x)| - 5 = 0 là
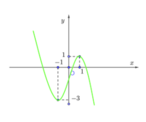
A. 3
B.5
C. 4
D. 6
Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình f(x)=3
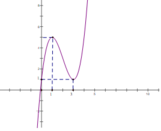
A. 0
B. 2
C. 1
D. 3
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2f(x)=3 là
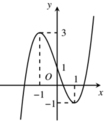
A. 3
B. 2
C. 1
D. 0
Cho hàm số y=f(x) có đồ thị như hình vẽ. Số nghiệm của phương trình 2 f ( x ) - 3 = 0 là
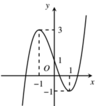
A. 3
B. 2
C. 1
D. 0
Cho hàm số y=f(x) có đồ thị như hình vẽ:
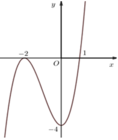
Tìm số nghiệm thực phân biệt của phương trình
f(x) = 1 + m 2
A. 2
B. 1
C. 0
D. 3
Cho hàm số y = f(x) có đồ thị như hình vẽ sau :
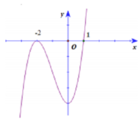
Tìm số nghiệm thực phân biệt của phương trình f(x) = 1
A. 0
B. 1
C. 3
D. 2
Đáp án B
Phương pháp:
Số nghiệm thực phân biệt của phương trình f(x) = 1 là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = 1
Cách giải: Dựa vào đồ thị hàm số ta thấy đường thẳng y = 1 cắt đồ thị hàm số y = f(x) tại 1 điểm duy nhất. Do đó f(x) = 1 có 1 nghiệm
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) = -3 có số nghiệm là
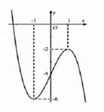
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f (x) có đồ thị như hình vẽ. Số nghiệm của phương trình f x + 1 - 1 = 3 4 là

A. 10
B. 12
C. 9
D. 8
Đặt ![]() phương trình trở thành:
f
t
=
3
4
phương trình trở thành:
f
t
=
3
4
Đồ thị hàm số |f(t)| được suy ra từ đồ thị hàm số f(t) bằng cách:
Giữ nguyên phần đồ thị trên trục hoành của f(t)
Lấy đối xứng qua trục hoành phần đồ thị dưới trục hoành của f(t)

Vì vậy đường thẳng y = 3 4 cắt đồ thị hàm số f(t) tại 6 điểm có hoành độ lần lượt a 1 < - 1 < a 2 < 0 < a 3 < a 4 < a 5 < a 6
Đối chiếu điều kiện t ≥ - 1 nhận các nghiệm t ∈ a 2 . . . a 6 Mỗi phương trình t = a i i = 2 , . . , 6 cho hai nghiệm phân biệt x. Vậy phương trình đã cho có tất cả 10 nghiệm thực.
Chọn đáp án A.