Cho khối lăng trụ tam giác ABC. A 1 B 1 C 1 có đáy là tam giác đều cạnh a, A 1 A = a 2 và A 1 A tạo với mặt phẳng (ABC) một góc 30 o Tính thể tích khối tứ diện A 1 B 1 C A là
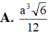
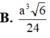
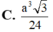
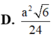
Cho khối lăng trụ ABC A'B'C' có đáy là tam giác đều cạnh a, điểm A' cách đều ba điểm A, B, C. Cạnh bên AA' tạo với mặt phẳng đáy một góc 60°. Thể tích khối lăng trụ ABC A'B'C' là
A. a 3 3
B. a 3 3 2
C. a 3 3 6
D. a 3 3 4
Thể tích khối lăng trụ :cho hình lăng trụ tam giác đều abc.a'b'c' có đáy là tam giác vuông tại b cạnh a'b' hợp với đáy 1 góc 30độ cạnh a'b'=a , a'c'=a căn 2 tính Vabc.a'b'c'
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB = a, AA'= 2a. Hình chiếu của A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A . a 3 11 4
B . a 3 11 12
C . a 3 47 8
D . 3 a 3 4
Đáp án A
Xét ∆AOA’, ta có:
AO2 + OA’2 = AA’2
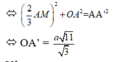
Vậy ![]()

Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh AB=a,AA'=2a . Hình chiếu của 'A lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ là:
A. a 3 11 4
B. a 3 11 12
C. a 3 47 8
D. a 3 4
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Tính thể tích khối lăng trụ ABC.A’B’C’
A . a 3 3 4
B . 4 a 3 3
C . 2 a 3 3
D . a 3 3 2
Đáp án C
Gọi M là trung điểm của BC suy ra ![]()
![]()
Lại có ![]()
![]()
![]()
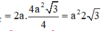
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Biết góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Tính thể tích khối lăng trụ ABC.A’B’C’
A. a 3 3 4
B. 4 a 3 3
C. 2 a 3 3
D. a 3 3 2
Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:
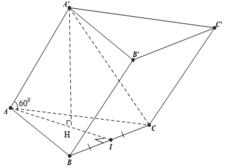
A. a 3 3 4
B. a 3 3 6
C. a 3 3 2
D. a 3 2 2
Đáp án A
Gọi I là giao điểm của AH và BC
Theo giả thiết H là trực tâm của tam giác đều ABC nên AH là đường cao và H cũng lả trọng tâm của tam giác đều ABC

Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, độ dài cạnh bên bằng 2 a 3 , hình chiếu của đỉnh A’ trên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Thể tích khối lăng trụ ABC.A’B’C’ bằng
A. a 3 3 36 .
B. a 3 3 6 .
C. a 3 3 12 .
D. a 3 3 24 .
Cho lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của điểm A′ lên mặt phẳng (ABC) trùng với tâm O của đường tròn ngoại tiếp tam giác ABC, biết O A ' = a . Tính theo a thể tích V của khối lăng trụ đã cho.
A. 3 a 3 4 .
B. 3 a 3 3 .
C. 3 a 3
D. 3 a 3 12
Đáp án C
V A B C . A ' B ' C ' = S A B C . O A ' = 3 a 3 .
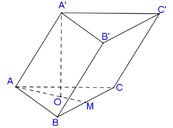
Cho hình lăng trụ ABC. A’B’C’ có đáy ABC là tam giác đều cạnh a, biết AA = AB = AC =a. Tính thể tích khối lăng trụ ABC.A’B’C’
A. 3 a 3 4
B. a 3 2 4
C. a 3 3 4
D. a 3 4