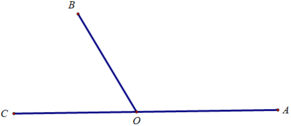
Cho hai góc AOB và BOC kề bù và B O C ^ = 1/2 A O B ^ .Tính số đo góc AOB.

Những câu hỏi liên quan
Hai góc AOB và BOC là 2 góc kề bù và hai góc BOC và COD cũng là 2 góc kề bù.
a,CMR:AOB và COD là 2 góc đối đỉnh
b,Biết BOC>AOB là 20 độ.Tính AOB và AOD
Cho 2 góc kề bù AOB và BOC biết AOB =55o
a. Vẽ A'OB' và B'OC' đối đỉnh với AOB và BOC
b. Tính A'OB' và A'OB
Cho widehat{AOB} và widehat{BOC} là hai góc kề bù . Biết widehat{BOC} 5 widehat{AOB} a) Tính số đo mỗi góc b) Gọi OD là tia nằm trong góc BOC sao chowidehat{BOD} 75^o . Tính góc AOD c) Trên cùng nửa mặt phẳng bờ là đường thẳng AC chứa tia OB,OD vẽ thêm n tia phân biệt gốc O ( không trùng với các tia OA,OB,OC,OD đã cho ) thì tất cả có bao nhiêu góc
Đọc tiếp
Cho \(\widehat{AOB}\) và \(\widehat{BOC}\) là hai góc kề bù . Biết \(\widehat{BOC}\) = 5 \(\widehat{AOB}\)
a) Tính số đo mỗi góc
b) Gọi OD là tia nằm trong góc BOC sao cho\(\widehat{BOD}\) = 75\(^o\) . Tính góc AOD
c) Trên cùng nửa mặt phẳng bờ là đường thẳng AC chứa tia OB,OD vẽ thêm n tia phân biệt gốc O ( không trùng với các tia OA,OB,OC,OD đã cho ) thì tất cả có bao nhiêu góc
a) Ta có: \(\widehat{AOB}\) và \(\widehat{BOC}\) là hai góc kề bù(gt)
nên \(\widehat{AOB}+\widehat{BOC}=180^0\)
\(\Leftrightarrow\widehat{AOB}+5\cdot\widehat{AOB}=180^0\)
\(\Leftrightarrow6\cdot\widehat{AOB}=180^0\)
hay \(\widehat{AOB}=30^0\)
Ta có: \(\widehat{BOC}=5\cdot\widehat{AOB}\)(gt)
nên \(\widehat{BOC}=5\cdot30^0\)
hay \(\widehat{BOC}=150^0\)
Vậy: \(\widehat{AOB}=30^0\); \(\widehat{BOC}=150^0\)
b) Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{DOB}< \widehat{BOC}\left(75^0< 150^0\right)\)
nên tia OD nằm giữa hai tia OB và OC
\(\Leftrightarrow\widehat{COD}+\widehat{BOD}=\widehat{COB}\)
\(\Leftrightarrow\widehat{COD}=\widehat{COB}-\widehat{BOD}=150^0-75^0=75^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OC, ta có: \(\widehat{COD}< \widehat{COA}\left(75^0< 180^0\right)\) nên tia OD nằm giữa hai tia OC và OA
\(\Leftrightarrow\widehat{COD}+\widehat{AOD}=\widehat{COA}\)
\(\Leftrightarrow\widehat{AOD}=\widehat{COA}-\widehat{COD}=180^0-75^0\)
hay \(\widehat{AOD}=105^0\)
Vậy: \(\widehat{AOD}=105^0\)
Đúng 1
Bình luận (0)
a) \(\widehat{AOB}\) và \(\widehat{BOC}\) kề bù \(\Rightarrow\widehat{AOB}+\widehat{BOC}=180^0\) mà \(\widehat{BOC}=5\widehat{AOB}\)
\(\Rightarrow\widehat{AOB}+5\widehat{AOB}=180^0\Rightarrow6\widehat{AOB}=180^0\\ \Rightarrow\widehat{AOB}=30^0\Rightarrow\widehat{BOC}=150^0\).
b) Do \(OD\) nằm trong góc \(\widehat{BOC}\) \(\Rightarrow\) tia \(OD\) nằm giữa hai tia \(OB,OC\)
\(\Rightarrow\)tia \(OB\) và tia \(OA\) nằm cùng phía nhau so với tia \(OD\)
\(\Rightarrow\) tia \(OB\) nằm giữa hai tia \(OA,OD\)
\(\Rightarrow\widehat{AOD}=\widehat{AOB}+\widehat{BOD}=30^0+75^0=105^0\).
c) Nếu chỉ xét trường hợp các góc tạo bởi hai tia liên tiếp nhau:
Trên nửa mặt phẳng bờ \(AC\) có \(n+4\) tia (gồm \(4\) tia \(OA,OB,OC,OD\) và \(n\) tia vẽ thêm).
Cứ hai tia cạnh nhau tạo thành 1 góc
\(\Rightarrow\) Ta có \(n+3\) góc.
Đúng 2
Bình luận (0)
Bài 1: Cho đường thẳng aa’ cắt bb’ tại O. Biết góc aOb’ =50 độ .Tính các góc còn lại?
Bài 2: Cho góc AOB=m độ. Vẽ hai góc BOC và AOD kề bù với AOB. Chứng minh rằng BOC và AOD đối đỉnh?
Bài 1: Cho đường thẳng aa’ cắt bb’ tại O. Biết góc aOb’ =50 độ .Tính các góc còn lại?
Bài 2: Cho góc AOB=m độ. Vẽ hai góc BOC và AOD kề bù với AOB. Chứng minh rằng BOC và AOD đối đỉnh?
Cho hai góc kề bù AOB và BOC. Biết AOB = 2BOC
Khi đó BOC =.......o
Ta có: AOB+BOC=180
Suy ra: AOB+2AOB=180
Suy ra: 3AOB=180
Suy ra: AOB=60
Suy ra: BOC=60x2=120 độ
Là 120 độ đó. Chắc chắn 10000000000000000000000000000000% luôn
Đúng 0
Bình luận (0)
ta có: AOB=2BOC (1)
AOB+BOC=180
thay (1) vào
=>2BOC+BOC=180
=>3BOC=180
=>BOC=60
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 2 góc kề bù AOB và góc BOC biết góc BOC -- góc AOB=80o . Tính 2 góc đó
Ta có: AOB+BOC=180o
BOC - AOB =80o
=> BOC>AOB
=> BOC= (180o+80o):2=130o
AOB= (180o-80o) :2=50o
Đúng 0
Bình luận (0)
BOC + AOB=1800
BOC - AOB =800
cộng 2 vế của 2 pt ta được 2BOC = 260 <=>BOC=130 =>AOB=50
hoặc giải như tìm 2 số biết tổng và hiệu của 2 số đó lớp 4 có học rồi ý
Đúng 0
Bình luận (0)
Ta có 2 góc AOB và góc BOC kề bù với nhau nên góc AOB + góc BOC = 180
mà góc BOC - góc AOB=80 nên suy ra
góc BOC= (180+80)/2 = 130
suy ra góc AOB= góc BOC - 80 = 130 - 80 = 50
k giùm mk vs nha
Đúng 0
Bình luận (0)
Cho hai góc AOB và BOC là hai góc kề bù và hai góc BOC và AOD cũng là hai góc kề bù.
a/ Chứng tỏ hai góc AOB và COD là hai góc đối đỉnh?
b/ Biết BOC lớn hơn góc AOB là 20 độ . Tính góc AOB và AOD?
Cho hai góc AOB và BOC kề bù và ∠BOC = 1/2 ∠AOB.Tính số đo góc AOB.
Ta có hai góc ∠BOC và ∠AOB kề bù nên ∠BOC + ∠AOB = 180o
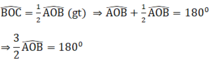
Đúng 0
Bình luận (0)




















