Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M(2 ; 1) qua phép đối xứng tâm I(3 ;-2).
A. M'(1;-3)
B. M'(-5;4)
C. M'(4;-5)
D. M'(1;5)
Trong mặt phẳng với hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M(2 ; 1) qua phép đối xứng tâm I(3 ;-2).
A. M’(1 ;-3)
B. M’ (-5 ; 4)
C. M’(4 ;-5)
D. M’(1 ;5)
Đáp án C
Phương pháp: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Cách giải: M và M’ đối xứng qua I nên I là trung điểm của MM’.
Ta có
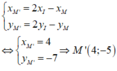
Trong mặt phẳng với hệ tọa độ Oxy, cho vectơ v → = ( 2 ; - 1 ) và điểm M(-3;1) Tìm tọa độ ảnh M' của điểm M qua phép tịnh tiến theo vectơ v → .
A. (5;3)
B. (1;-1)
C. (-1;1)
D. (1;1)
Bài 1. Trong mặt phẳng tọa độ Oxy cho điểm M(4;-3) và vectơ u ( -2;1). Qua phép tịnh tiến theo vecto u:
1) Tìm tọa độ điểm M' là ảnh của M
2) Tìm tọa độ điểm A biết M là ảnh của A
3) Tìm đường thẳng d' là ảnh của d: 3x - 4y +5 = 0
4) Tìm đường thẳng d1với d2 là ảnh của d1.
5) Tìm đường thẳng d5 là ảnh của d4: x + 2y +9 =0
6) Tìm đường tròn (C') là ảnh của (C): x2 + y2 -4x + 6y -7 =0
Bài 1. Trong mặt phẳng tọa độ Oxy cho điểm M(4;-3) và vectơ u ( -2;1). Qua phép tịnh tiến theo vecto u:
1) Tìm tọa độ điểm M' là ảnh của M
2) Tìm tọa độ điểm A biết M là ảnh của A
3) Tìm đường thẳng d' là ảnh của d: 3x - 4y +5 = 0
4) Tìm đường thẳng d1với d2 là ảnh của d1.
5) Tìm đường thẳng d5 là ảnh của d4: x + 2y +9 =0
6) Tìm đường tròn (C') là ảnh của (C): x2 + y2 -4x + 6y -7 =0
Trong không gian với hệ tọa độ Oxyz, cho điểm M 2 ; − 1 ; 1 . Tìm tọa độ điểm M¢ là hình chiếu vuông góc của M trên mặt phẳng (Oxy)
A. M ' 2 ; − 1 ; 0
B. M ' 0 ; 0 ; 1
C. M ' − 2 ; 1 ; 0
D. M ' 2 ; 1 ; − 1
Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .
Trong mặt phẳng tọa độ Oxy cho vecto v → = 1 ; 2 . Tìm tọa độ của điểm M’ là ảnh của điểm M 3 ; - 1 qua phép tịnh tiến T v → .
Ta có M(x^',y') là ảnh của M qua phép tịnh tiến theo vecto v→
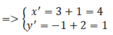
⇒ M(4;1)
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ u → và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. (1;5)
B. (-4;2)
C. (5;3)
D. (0;1)
trong mặt phẳng tọa độ OXY cho điểm M(2:1). Tìm tọa độ ảnh của M qua phép vị tự
a)V(O,-2)
b)V(1,4) với I (-1,3)
Lời giải:
Gọi $M'(a,b)$ là ảnh của $M$ qua phép vị tự $V,I$
a. Ta có:
\(\overrightarrow{OM'}=-2\overrightarrow{OM}\Leftrightarrow (a,b)=-2(2,1)=(-4,-2)\)
Vậy $M'(-4,-2)$
b. \(\overrightarrow{IM'}=4\overrightarrow{IM}\Leftrightarrow (a+1,b-3)=4(3, -2)\)
\(\Leftrightarrow \left\{\begin{matrix} a+1=4.3=12\\ b-3=4(-2)=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=11\\ b=-5\end{matrix}\right.\)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(2;-1;4). Gọi H là hình chiếu vuông góc của M lên mặt phẳng (Oxy). Tọa độ điểm H là:
A. H(2;0;4)
B. H(0;-1;4)
C. H(2;-1;0)
D. H(0;-1;0).
Đáp án C
Do chiếu xuống (Oxy) nên z=0 và x,y giữ nguyên.