1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Tập nghiệm của bất phương trình 3 - 2 x + 2 - x < x + 2 - x là
A. 1 ; 2
B. ( 1 ; 2 ]
C. - ∞ ; 1
D. ( - ∞ ; 1 ]
Tập nghiệm của bất phương trình 3 - 2 x + 2 - x < x + 2 - x là:
A. S = ( 1 ; 2 )
B. S = ( 1 ; 2 ]
C. S = ( - ∞ ; 1 )
D. S = ( - ∞ ; 1 ]
Điều kiện: x ≤ 2
Với điều kiện trên ,bất phương trình đã cho trở thành:
3- 2x < x ⇔ - 3 x < - 3 ⇔ x > 1
Kết hợp điều kiện ta được: 1 < x ≤ 2
Tập nghiệm của bất phương trình là S = (1; 2]
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x
A. 0 ; 2 .
B. 2 ; + ∞ .
C. − 2 ; − 1 .
D. 0 ; + ∞ .
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x
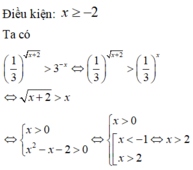
Kết hợp điều kiện, vậy tập nghiệm của bất phương trình là S = 2 ; + ∞
Đáp án A
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x
A. 2 ; + ∞
B. 1 ; 2
C. ( 1 ; 2 ]
D. [ 2 ; + ∞ )
Tập nghiệm của bất phương trình 2 x + 2 > 3 ( 2 - x ) + 1 là:
A. S = 1 ; + ∞
B. S = - ∞ ; - 5
C. S = 5 ; + ∞
D. S = - ∞ ; 5
Ta có :
2 x + 2 > 3 ( 2 - x ) + 1 ⇔ 2 x + 2 > 6 - 3 x + 1 ⇔ 5 x > 5 ⇔ x > 1 .
Vậy tập nghiệm của bất phương trình 2 x + 2 > 3 ( 2 - x ) + 1 là 1 ; + ∞ .
Đáp án là A.
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 - x là
A. 1 , 2 .
B. 2 , + ∞ .
C. [ 2 , + ∞ ) .
D. ( 1 , 2 ]
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x là
A. (1;2)
B. 2 , + ∞ .
C. 2 , + ∞ .
D. 1 , 2 .
Tập nghiệm của bất phương trình 1 3 x + 2 > 3 − x là
A. 0 ; 2 .
B. 2 ; + ∞ .
C. − 2 ; − 1 .
D. 0 ; + ∞ .
Đáp án B
1 3 x + 2 > 3 − x ⇔ x + 2 ≥ 0 3 − x + 2 > 3 − x ⇔ x ≥ − 2 x + 2 < x ⇔ x ≥ − 2 x > 0 x + 2 < x 2 ⇔ x > 0 x + 1 x − 2 > 0
⇔ x > 0 x > 2 x < − 1 ⇔ x > 2
Vậy tập nghiệm của bất phương trình S = 2 ; + ∞ .
