Cho hàm số y = f ( x ) = x 3 - 3 x 2 + 2 có đồ thị như hình vẽ bên. Trong bốn đường cong dưới đây, đường nào là đồ thị của hàm số y = x + 1 ?
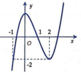
A. 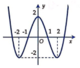
B. 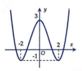
C. 
D. 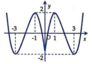
Cho hàm số f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên và f(-2)=f(2)=0. Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
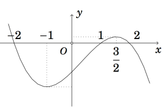
A. (1;2).
B. (-2;-1).
C. ( 5 ; + ∞ ) .
D. (2;5).
Câu 23: Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị như hình vẽ bên. Hàm số y = f(3 - 2x) tăng trên khoảng nào:

Hình 3: Đồ thị y=f(x)

Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
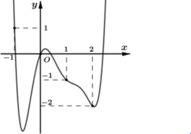
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
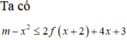
![]()
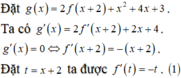
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
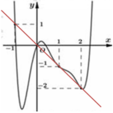
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



Cho hàm số y = f ( x ) có đồ thị y = f ' ( x ) như hình vẽ bên. Đồ thị hàm số g ( x ) = 2 f ( x ) - ( x - 1 ) 2 có tối đa bao nhiêu điểm cực trị?
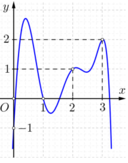
A. 3
B. 5
C. 6
D. 7
Cho hàm số y = f(x). Hàm số y = f'(x) có đồ thị như hình vẽ bên. Hỏi hàm số y = f(x-3) đồng biến trên khoảng nào sau đây:
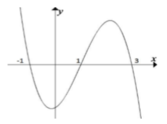
A. (2;4).
B. (1;3).
C. (-1;3).
D. (5;6).
Chọn D.
Nhận xét: Từ đồ thị f'(x) , ta có 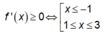
Từ đó 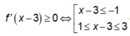
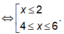
Do đó chọn D.
Cho hàm số y = f(x). Biết hàm số y = f(x) có đồ thị như hình vẽ bên dưới. Hàm số y = 3 - x 2 đồng biến trên khoảng
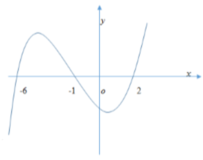
A. (0;1)
B. (-1;0)
C. (2;3)
D. (-2;-1)
Cho hàm số f (x) có đồ thị của hàm số y = f'(x-2)+2 như hình vẽ bên.
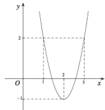
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây ?
A. - ∞ ; 2
B. - 1 ; 1
C. 3 2 ; 5 2
D. 2 ; + ∞
Cho hàm số f (x) có đồ thị của hàm số y=f'(x-2)+2 như hình vẽ bên.
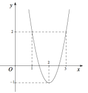
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây ?
A. ( - ∞ ; 2 ) .
B. (-1;1).
C. 3 2 ; 5 2 .
D. ( 2 ; + ∞ ) .
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f(x) = -3 có số nghiệm là
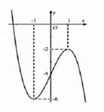
A. 0
B. 1
C. 2
D. 3
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30