Cho số thực a>0 và a ≠ 1 . Hãy rút gọn biểu thức P = a 1 3 a 1 2 - a 5 2 a 1 4 a 7 12 - a 19 12
Những câu hỏi liên quan
Cho số thực
a
0
và
a
≠
1
. Hãy rút gọn biểu thức
P
a
1
3
a
1
2
−
a
5...
Đọc tiếp
Cho số thực a > 0 và a ≠ 1 . Hãy rút gọn biểu thức P = a 1 3 a 1 2 − a 5 2 a 1 4 a 7 12 − a 19 12
A. P = 1+ a
B. P = 1
C. P = a
D. P = 1 - a
ĐỀ 1Bài 1: (3,0 điểm) 1. Thực hiện các phép tính: a) 2. Không dùng máy tính và bảng số hãy so sánh: 5 và Bài 2: (3,0 điểm) Rút gọn các biểu thức sau: a) b) c) Bài 3: (3,5 điểm) Cho biểu thức với x ³ 0 và x ¹ 1. a) Chứng minh: b) Tính giá trị của A khi c) Tìm các giá trị của x sao cho Bài 4: (0,5 điểm)Tìm giá trị nhỏ nhất của biểu thức:B với x 2017
Đọc tiếp
ĐỀ 1
Bài 1: (3,0 điểm)
1. Thực hiện các phép tính:
a) 
2. Không dùng máy tính và bảng số hãy so sánh: 5 và 
Bài 2: (3,0 điểm) Rút gọn các biểu thức sau:
a) 
b) 
c) 
Bài 3: (3,5 điểm)
Cho biểu thức 
với x ³ 0 và x ¹ 1.
a) Chứng minh: 
b) Tính giá trị của A khi 
c) Tìm các giá trị của x sao cho 
Bài 4: (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức:
B = 
với x > 2017
1. Cho biểu thức A=(-a-b+c)-(-a-b-c). Hãy rút gọn biểu thức A
2.Tìm tất cả các số nguyên a biết (6a+1) chia hết cho (3a-1)
3.Tìm số nguyên a,b biết a>0 và a(b-2)=3
4.Chứng minh rằng nếu 2 số a,b là 2 số nguyên khác 0 và a là bội của b;b là bội của a thì a=b hoặc a=-b
Cho a lớn hơn hoặc bằng 0 và a khác 1 . Hãy rút gọn biểu thức sau A = \(\left(\frac{1-a\sqrt{a}}{1-\sqrt{a}}\right)\left(\frac{1-\sqrt{a}}{1-a}\right)^2\)
\(A=\left(\frac{1-\left(\sqrt{a}\right)^3}{1-\sqrt{a}}\right)\left(\frac{1-\sqrt{a}}{1-\left(\sqrt{a}\right)^2}\right)^2\)
\(=\left(1+\sqrt{a}+a\right).\frac{1}{\left(1+\sqrt{a}\right)^2}\)
\(=\frac{1+\sqrt{a}+a}{1+2\sqrt{a}+a}\)
Đúng 0
Bình luận (0)
Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Đọc tiếp
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó
Cho a là số thực dương. Viết và rút gọn biểu thức
a
3
2018
.
a
2018
dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó. A.
2
1009
B.
1
1009
C.
3
1009
D.
3...
Đọc tiếp
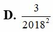
Cho a là số thực dương. Viết và rút gọn biểu thức a 3 2018 . a 2018 dưới dạng lũy thừa với số mũ hữu tỉ. Tìm số mũ của biểu thức rút gọn đó.
A. 2 1009
B. 1 1009
C. 3 1009
D. 3 2018 2
2) Cho số thực alpha <= 1 . Rút gọn biểu thức P= sqrt 15 2 - sqrt 10. (a - 1) ^ 2 3 .
cho biểu thức sau:A=(1/x-2-2x/4-x^2+1/2+x)*(2/x-1).
hãy rút gọn và tính giá trị biểu thức tại x thỏa mãn 2x^2+x=0,
tìm x để A=1/2,tìm x nguyên để A nguyên dương