Có bao nhiêu nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện 0 < x < π
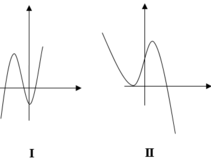
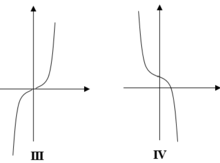
A. Đồ thị (III) xảy ra khi
B. Đồ thị (IV) xảy ra khi
C. Đồ thị (II) xảy ra khi
D. Đồ thị (I) xảy ra khi
Phương trình sin 2 x = - 1 2 có bao nhiêu nghiệm thỏa mãn 0 < x < π
A. 1
B. 3
C. 2
D. 4
tìm m sao cho phương trình \(\frac{2sinx-1}{sin+3}=m\) có đúng 2 nghiệm thỏa mãn điều kiện \(0\le x\le\pi\)
tìm m sao cho phương trình \(\frac{2\sin x-1}{\sin x+3}=m\) có đúng 2 nghiệm thỏa mãn điều kiện 0≤x≤π
Có bao nhiêu giá trị nguyên của tham số m để phương trình sin 2 x + cos 2 x + | sin x + cos x | - cos 2 x + m - m = 0 có nghiệm thực?
A. 9
B. 2
C. 3
D. 5
Đáp án C
Sử dụng tính đơn điệu của hàm số, đánh giá số nghiệm của phương trình.
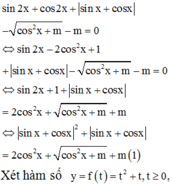
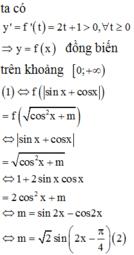

Vậy, có 3 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
Có bao nhiêu giá trị nguyên của m để phương trình: sin2x + 2 sin(x + π 4 ) - m = 0 có nghiệm.
A.3
B.4
C.5
D.6
Nghiệm của phương trình cos2 x- cosx = 0 thỏa mãn điều kiện 0 < x < π
A. x= π / 6
B. x= π / 2
C. x= π / 4
D. x=- π / 2
Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0
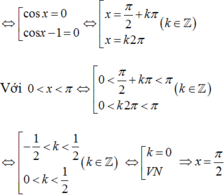
Phương trình sin 2x + 3cos x =0 có bao nhiêu nghiệm trong khoảng 0 ; π
A. 0
B. 1
C. 2
D. 3
Cho hệ phương trình: x+ay=2 và ax-27=1. Tìm các giá trị của a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện x>0, y<0.
Cho hệ phương trình :
x + a y = 3 a x - y = 2
b) Tìm điều kiện của a để hệ phương trình có nghiệm duy nhất thỏa mãn x + y > 0
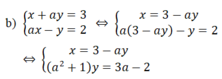
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
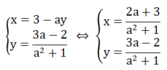
Khi đó:
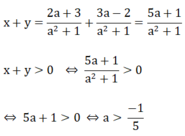
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0