Xét các mệnh đề sau
1 . ∫ 1 1 − 2 x d x = − 1 2 ln 4 x − 2 2 . ∫ 2 x ln x + 2 d x = x 3 − 4 ln x + 2 − ∫ x − 2 d x 3 . ∫ 1 sin 2 x d x = − cot 2 x 2 + C
Số mệnh đề đúng là
A. 2
B. 0
C. 3
D. 1
Những câu hỏi liên quan
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sauTrong ba mệnh đề (I),(II),(III), số mệnh đề sai là A. 2 B. 0 C. 3 D. 1
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
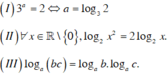
Trong ba mệnh đề (I),(II),(III), số mệnh đề sai là
A. 2
B. 0
C. 3
D. 1
Cho tập hợp A={1, 2, 3, 4, a, b}. Xét các mệnh đề sau đây:
(I): “3 ∈ A”.
(II): “{3, 4} ∈ A”.
(III): “{a, 3, b} ∈ A”.
Trong các mệnh đề sau, mệnh đề nào đúng
A. I đúng
B. I,II đúng
B. I,II đúng
B. I,II đúng
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∀ x ∈ R : x < x + 1
C: “∀ x ∈ R : x < x + 1”.
C− : “∃ x ∈ R: x ≥ x + 1”.
C− sai vì x + 1 luôn lớn hơn x.
Đúng 1
Bình luận (0)
Xét tính chất chẵn lẻ của hàm số y = 2 x 3 + 3x + 1. Trong các mệnh đề sau, tìm mệnh đề đúng?
A. y là hàm số chẵn
B. y là hàm số lẻ.
C. y là hàm số không có tính chẵn lẻ
D. y là hàm số vừa chẵn vừa lẻ
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ R: 3x = x2 + 1
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với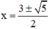 
D− thỏa mãn:
Đúng 0
Bình luận (0)
Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng? A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau. B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau. C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songvới nhau. D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.
Đọc tiếp
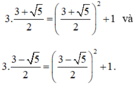
Xét các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
A. Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song songvới nhau.
D. Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau.
Đáp án là C
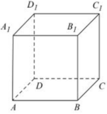
“Hai mặt phẳng cùng vuông góc với một mặt phẳng thì song song với nhau” và mệnh đề “Hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ ba thì song song với nhau” là mệnh đề sai, ví dụ trong hình lập phương trên ta có ( C 1 B 1 BC) và ( D 1 B 1 BD) cùng vuông góc với (ABCD) nhưng 2 mặt phẳng đó lại cắt nhau.
“Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau” là mệnh đề sai ví dụ như trong hình lập phương trên ta có A 1 B 1 và C 1 B 1 cùng vuông góc với B1B nhưng A 1 B 1 ⊥ C 1 B 1
“Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau” là mệnh đề đúng .
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
I
3
a
2
⇔
a
log
3
2
I
I
∀
x
∈
ℝ
0
,
log
2
x
2...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
(
I
)
3
a
2
⇔
a
log
3
2
(
II
)
∀
x
∈
R
{
0
}
,
log
2
x
2
2
log...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
( I ) 3 a = 2 ⇔ a = log 3 2
( II ) ∀ x ∈ R \ { 0 } , log 2 x 2 = 2 log 2 x
( III ) log a ( bc ) = log a b . log a c
Trong ba mệnh đề (I), (II), (III) số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a, b, c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau:(I)
2
a
3
⇔
a
log
2
3
(II)
∀
x
∈
ℝ
0
,
log
3
x
2
2
log
3
x
(III) ...
Đọc tiếp
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log 3 x 2 = 2 log 3 x khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 là chưa đủ.
Mệnh đề (III) sai vì log a b . c = log a b + log a c
Số mệnh đề đúng là 1.
Đúng 0
Bình luận (0)