Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 2 x - 1 2 , trục hoành và các đường thẳng x = 2 và x = 8.
A. 12 7
B. 9
C. 12
D. 10
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
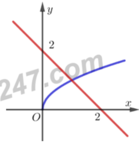
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số y = x2 + x; y = 2x.
A. 1 3
B. 1 6
C. 2 3
D. π 6
Tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số y = x 2 + x , y = 2 x
A. 1 3
B. 1 6
C. 2 3
D. π 6
Tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số y = x 2 + x , y = 2 x .
A. V = 5 R 3
B. V = 4 R 3
C. V = 2 R 3
D. V = 3 R 3
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x − 1 và đường thẳng y = 2.
A. 12
B. 4
C. 6
D. 2
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x 3 - x và đồ thị hàm số y = x - x 2
A. 9 4
B. 37 12
C. 81 12
D. 13
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x 3 - x = x - x 3 <=> x 3 + x 2 - 2 x = 0
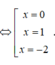
Vậy diện tích của hình phẳng tính là
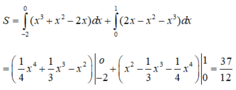
Vậy chọn đáp án B.
Tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số y=2x^ 3 -3x^ 2 +1 và y = x ^ 3 - 4x ^ 2 + 2x + 1 .
Phương trình hoành độ giao điểm:
\(2x^3-3x^2+1=x^3-4x^2+2x+1\)
\(\Leftrightarrow x^3+x^2-2x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\\x=1\end{matrix}\right.\)
Trên \(\left(-2;0\right)\) ta có \(x^3+x^2-2x>0\) và trên \(\left(0;1\right)\) ta có \(x^3+x^2-2x< 0\)
Do đó:
\(S=\int\limits^0_{-2}\left(x^3+x^2-2x\right)dx-\int\limits^1_0\left(x^3+x^2-2x\right)dx=\dfrac{8}{3}+\dfrac{5}{12}=\dfrac{37}{12}\)
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 8 x + 1 và đường thẳng y = x + 2 .
A. 1 12
B. 1 6
C. 1 3
D. 1 2
Chọn B
Phương trình hoành độ giao điểm :

Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 1 - 1 x 2 , trục hoành và đường thẳng x = 1 và đường thẳng x = 2.
A. 0,3
B. 0,2
C. 0,4
D. 0,5
Tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = 1 - 1 x 2 , trục hoành và đường thẳng x = 1 và đường thẳng x = 2
A. 0,3
B. 0,2
C. 0,4
D. 0,5