Cho hai hàm số f(x) và g(x) có đồ thị như hình vẽ dưới đây
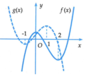
Biết rằng hai hàm số y = f - 2 x + 1 và y = 3 g a x + b a , b ∈ Q có cùng khoảng đồng biến. Giá trị của biểu thức a + 2 b bằng
A. a + 2 b = 3
B. a + 2 b = 4
C. a + 2 b = 2
D. a + 2 b = 6
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
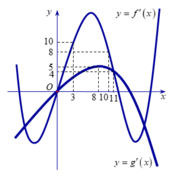
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hai hàm số đa thức bậc bốn y=f(x)và y=g(x) có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số y=f(x). Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là -3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là -1 và 3. Giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [-3;3] bằng
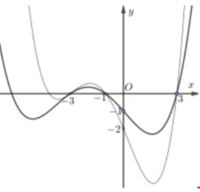
A. 12 - 8 3 9
B. - 3
C. 12 - 10 3 9
D. 10 - 9 3 9
Theo giả thiết có ![]()
![]()
Do ![]()
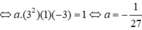
Do đó ![]()
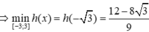
Chọn đáp án A.
Cho hai hàm số y=f(x), y=g(x) có đạo hàm là f '(x), g'(x). Đồ thị hàm số y=f '(x) và y=g(x) được cho như hình vẽ bên dưới.
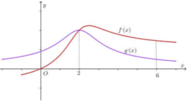
Biết rằng f 0 - f 6 < g 0 - g 6 . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h x = f x - g x trên đoạn 0 ; 6 lần lượt là:
A. h 2 ; h 6
B. h 6 ; h 2
C. h 0 ; h 2
D. h 2 ; h 0
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
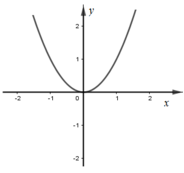
Cho hàm số y = f(x) và y = g(x) có đồ thị lần lượt như hình vẽ
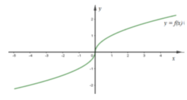
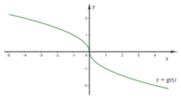
Đồ thị hàm số y = f(x).g(x) là đồ thị nào dưới đây?
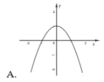
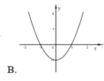
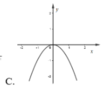
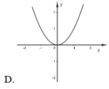
Đáp án C.
Cách giải:
Đặt y = f(x).g(x) = h(x). Khi đó:
h(0) = f(0).g(0) = 0.0 = 0
h(1) = f(1).g(1) = 1.(-1) = -1
Do đó, ta chọn phương án C
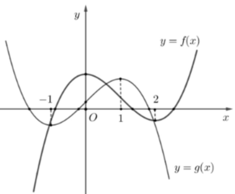
Cho hai hàm số y=f(x); y=g(x) có đạo hàm trên R và có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Biết rằng hai hàm số y=f(-2x+1) và y = g a x + b a b ∈ ℝ ; a # 0 có cùng khoảng đồng biến. Giá trị của a + 2b bằng
A. 3
B. 4
C. 2
D. 6
Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 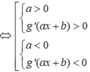
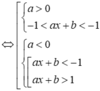
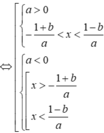
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
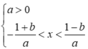 và
và 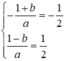
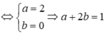
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.
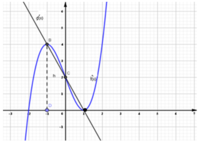
Cho hai hàm số y = f(x) và y = g(x) có đồ thị của hàm y = f '(x), y = g'(x) như hình vẽ. Tìm các khoảng đồng biến của hàm số y = f(x) - g(x)
A. - 1 ; 0 ; 1 ; + ∞
B. - ∞ ; - 1 ; 0 ; 1
C. 1 ; + ∞ ; - 2 ; - 1
D. - 2 ; + ∞
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
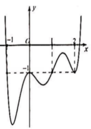
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f’(x) như hình vẽ bên dưới. Hỏi đồ thị hàm số g(x)=-x-f(x) đạt cực đại tại?
A. x = -1
B. x = 0
C. x = 1
D. x = 2