Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc B A D ⏜ = 60 0 , SA=SB=SB= a 3 2 . Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3
Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc
BAC
^
60
°
,
SO
⊥
(
ABCD
)
và SO 3a/4. Tính thể tích khối chóp S.ABCD. A.
a
3
3
8
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAC ^ = 60 ° , SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
A. a 3 3 8
B. a 3 3 4
C. a 3 4
D. 3 a 3 3 8
8 tháng 6 2021 lúc 21:13
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAD = 60 ° với AC cắt BD tại O, SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
Lời giải:
$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$
$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$
$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$
$BD=2BO=a$
$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AO=\frac{\sqrt{3}a}{2}$
$\Rightarrow AC=\sqrt{3}a$
$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$
$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc
B
A
D
^
60
°
có SO vuông góc mặt phẳng (ABCD) và SO a, Khoảng cách từ O đến mặt phẳng (SBC) là A.
a
57
3
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc B A D ^ = 60 ° có SO vuông góc mặt phẳng (ABCD) và SO = a, Khoảng cách từ O đến mặt phẳng (SBC) là
A. a 57 3
B. a 3 4
C. a 57 19
D. 2 a 3
Đáp án C
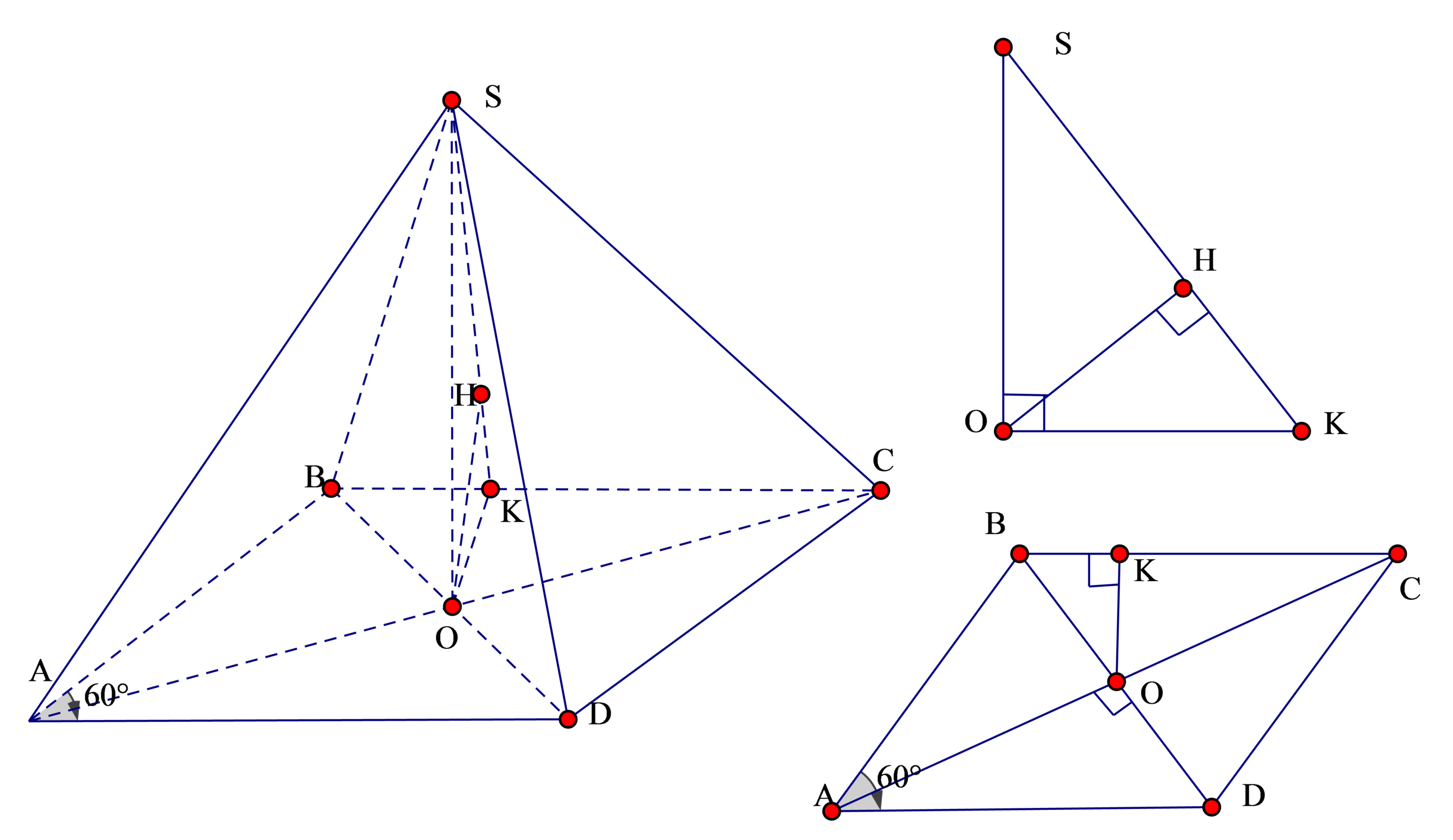
Kẻ O K ⊥ B C , O H ⊥ S K như hình vẽ khi đó OH là khoảng cách từ O tới (SBC)
Dễ thấy Δ A B D đều
⇒ O K = O B . sin 60 0 = a 2 . 3 2 = a 3 4
Ta có: 1 O H 2 = 1 O K 2 + 1 S O 2 = 16 3 a 2 + 1 a 2 = 19 3 a 2
⇒ O H = a 57 19
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, ABa,
B
A
D
^
60
°
SO
⊥
(ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc
60
°
. Tính thể tích khối chóp S.ABCD A.
V
S
.
A
B
C
D
...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB=a, B A D ^ = 60 ° SO ⊥ (ABCD) và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp S.ABCD
A. V S . A B C D = 3 a 3 12
B. V S . A B C D = 3 a 3 24
C. V S . A B C D = 3 a 3 8
D. V S . A B C D = 3 a 3 48
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc
B
A
D
60
°
,
có SO vuông góc với mặt phẳng (ABCD) và SO a Khoảng cách từ O đến mặt phẳng (SBC) là: A.
a
57
19
B.
a
57
18...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc B A D = 60 ° , có SO vuông góc với mặt phẳng (ABCD) và SO = a Khoảng cách từ O đến mặt phẳng (SBC) là:
A. a 57 19
B. a 57 18
C. a 45 7
D. a 52 16
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc
B
A
C
^
60
°
. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Mặt phẳng (SAC) hợp với mặt phẳng (ABCD) một góc 450. Thể tích khối chóp S.ABCD bằng A.
a
3
12
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc B A C ^ = 60 ° . Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Mặt phẳng (SAC) hợp với mặt phẳng (ABCD) một góc 450. Thể tích khối chóp S.ABCD bằng
A. a 3 12
B. a 3 6
C. a 3 3
D. a 3 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc
B
A
D
⏜
có số đo bằng
60
°
. Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng
60
°
. Tính khoảng cách từ B đến mặt phẳng (SCD) . A.
3
a
17...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc B A D ⏜ có số đo bằng 60 ° . Hình chiếu của S lên mặt phẳng (ABCD) là trọng tâm tam giác ABC .Góc giữa (ABCD) và (SAB) bằng 60 ° . Tính khoảng cách từ B đến mặt phẳng (SCD) .
A. 3 a 17 14
B. 3 a 7 14
C. 3 a 17 4
D. 3 7 4
Đáp án B
Gọi H là trọng tâm Δ A B C
Dựng H K ⊥ A B , H E ⊥ C D , H F ⊥ S E
Ta có A B ⊥ S H K ⇒ S K H ⏜ = 60 °
Do đó S H = H K tan 60 °
Mặc khác H K = H B sin 60 ° ( Do Δ A B C là tam giác đều nên A B D ⏜ = 60 ° ) suy ra H K = a 3 sin 60 ° = a 3 6 ⇒ S H = a 2
Lại có H E = H D tan 60 ° = a 3 3 ⇒ H F = a 7 = d H ; S C D
Do đó B D H D = 3 2 ⇒ d B = 3 2 d H = 3 a 17 14
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng
60
o
,
O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng
45
o
.
Tính theo a thể tích khối chóp SABCD. A.
3
2
a
3
x B.
a
3
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng 60 o , O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 45 o . Tính theo a thể tích khối chóp SABCD.
A. 3 2 a 3 x
B. a 3 4
C. 3 a 3 8
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O,
A
B
a
,
B
A
D
^
60
°
,
S
O
⊥
A
B
C
D
và mặt phẳng (SCD) tạo với mặt đáy một góc
60
°
.
Tính thể tích khối chóp A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, A B = a , B A D ^ = 60 ° , S O ⊥ A B C D và mặt phẳng (SCD) tạo với mặt đáy một góc 60 ° . Tính thể tích khối chóp
A. V S . A B C D = 3 a 3 24
B. V S . A B C D = 3 a 3 8
C. V S . A B C D = 3 a 3 12
D. V S . A B C D = 3 a 3 48
Cho hình chóp
S
.
A
B
C
D
có đáy
A
B
C
D
là hình thoi cạnh a, góc
B
A
C
⏜
60
°
, hình chiếu của đỉnh S trên mặt phẳng
A
B
C
D
trùng với trọng tâm tam giác
A
B...
Đọc tiếp
Cho hình chóp S . A B C D có đáy A B C D là hình thoi cạnh a, góc B A C ⏜ = 60 ° , hình chiếu của đỉnh S trên mặt phẳng A B C D trùng với trọng tâm tam giác A B C , góc tạo bới hai mặt phẳng S A C và A B C D là 60 ° . Khoảng cách từ B đến mặt phẳng S C D theo a bằng
A. 3 a 2 7
B. 9 a 2 7
C. a 2 7
D. 3 a 7
Đáp án là A.
d B ; S C D = 3 2 d G ; S C D
Tính được: G H = a 3 3 ; S G = a 2 ; G K = a 7 .
Vậy d B ; S C D = 3 2 d G ; S C D = 3 2 . a 7 = 3 a 2 7 .
Đúng 0
Bình luận (0)