Tính tổng tất cả các nghiệm của phương trình tan x + c o t x = 4 3 3 trên đoạn 0 ; π
A. π 2
B. 3 π 2
C. π 3
D. 2 π 3
Tính tổng tất cả các nghiệm của phương trình e sin x - π 4 = tan x thuộc đoạn 0 ; 50 π ?
A. 1853 π 2
B. 2475 π 2
C. 2671 π 2
D. 2105 π 2
Đáp án B
Điều kiện: tan x > 0
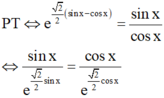
Xét hàm số y = f t = t e 2 2 t t ∈ - 1 ; 1
Khi đó f ' t = e 2 2 1 - t 2 2 e 2 t > 0 ∀ t ∈ - 1 ; 1
do đó hàm số f(t) đồng biến trên [–1;1]
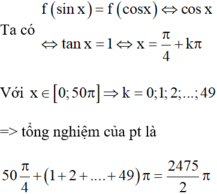
Tính tổng T tất cả các nghiệm của phương trình
( x - 3 ) 2 x 2 - 5 x = 1 .
A. T = 0
B. T = 4
C. T = 13 2
D. T = 15 2
Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
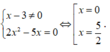
Vậy phương trình đã cho có ba nghiệm
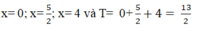
Chọn C.
Tính tổng T tất cả các nghiệm của phương trình log 5 25 - 5 x + x - 3 = 0 .
A.1
B.3
C.25
D.2
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Tính tổng tất cả các nghiệm của phương trình sin 2 x + 4 sin x - 2 cos x - 4 = 0 trong đoạn [ 0 ; 100 π ] của phương trình:
A . 2476 π
B . 25 π
C . 2475 π
D . 100 π
Câu 1: Tính tổng tất cả các nghiệm của phương trình sin3(\(x-\dfrac{\pi}{4}\)) = \(\sqrt{2}\)sinx trên đoạn [0 ; 2018]
Câu 2: Tính tổng tất cả các nghiệm của phương trình cos2x (tan2x - cos2x) = cos3x - cos2x + 1 trên đoạn [0 ; 43π]
GIÚP MÌNH VỚI!!!![]()
Tất cả các nghiệm của phương trình tan x + 3 . c o t x - 3 - 1 = 0 là

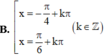
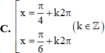
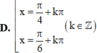
Tính S là tổng tất cả các nghiệm của phương trình 4( 22x + 2-2x)– 4( 2x + 2-x) - 7 = 0.
A. S = 1
B. S = -1
C. S = 3
D. S = 0
Chọn D.
Đặt t = 2x + 2-x, suy ra t2 = 22x + 2 -2x + 2.
Ta có ![]()
Phương trình trở thành
![]()
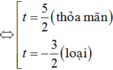
![]()
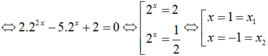
khi đó ; S = x1+ x2 = 0.
Tính tổng T tất cả các nghiệm của phương trình 4 x - 8 . 2 x + 4 = 0
A. T = 1
B. T = 2
C. T = 8
D. T = 0
Tất cả các nghiệm của phương trình tan x = c o t x là
A. x = π 4 + k π 4 , k ∈ ℤ
B. x = π 4 + k 2 π , k ∈ ℤ
C. x = π 4 + k π , k ∈ ℤ
D. x = π 4 + k π 2 , k ∈ ℤ