Cho lăng trụ ABC.A’B’C’ có khoảng cách từ điểm A đến mặt phẳng (A’BC) bằng 6a. Khoảng cách từ trung điểm M cạnh B’C’ đến mặt phẳng (A’BC) bằng
A. 2a.
B. 4a.
C. 6a.
D. 3a.
Cho lăng trụ ABC.A’B’C’ có khoảng cách từ điểm A đến mặt phẳng (A’BC) bằng 6a. Khoảng cách từ trung điểm M cạnh B’C’ đến mặt phẳng (A’BC) bằng
A. 2a.
B. 4a.
C. 6a.
D. 3a.
Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của CC’. Khoảng cách từ M đến mặt phẳng (A’BC) bằng
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
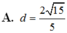
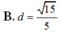
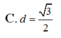
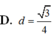
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
A. d = 2 15 5
B. d = 15 5
C. d = 3 2
D. d = 3 4
Chọn B
Gọi M là trung điểm của BC và H là hình chiếu vuông góc của A trên đường thẳng A’M
Khi đó
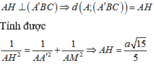
Cho hình lăng trụ đều ABC.A’B’C’ có góc giữa đường thẳng A’B với mặt phẳng (ABC) bằng 60 ° và khoảng cách từ điểm A đến mặt phẳng (A’BC) bằng a 5 2 . Tính theo a thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 125 3 96 a 3 .
B. V = 125 3 288 a 3 .
C. V = 125 3 384 a 3 .
D. V = 125 3 48 a 3 .
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Khoảng cách từ A đến mặt phẳng (A’BC) bằng
A. a 2 2
B. a 6 4
C. a 21 2
D. a 3 4
Đáp án C

Gọi E là trung điểm của BC, F là hình chiếu của A xuống A’E
Dễ chứng minh F là hình chiếu của A xuống mp (A’BC)
Khi đó:
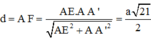 trong đó AE =
a
3
2
trong đó AE =
a
3
2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=a, AA’=2a. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC).
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
Cho lăng trụ tam giác A B C . A ' B ' C ' có khoảng cách từ A đến mặt phẳng A ' B C bằng 6a Khoảng cách từ trung điểm M của cạnh B ' C ' đến mặt phẳng A ' B C bằng
A. 6a
B. 2a
C. 4a
D. 3a
Cho lăng trụ tam giác ABC.A'B'C' có khoảng cách từ A đến mặt phẳng (A'BC) bằng 6a. Khoảng cách từ trung điểm M của cạnh B'C' đến mặt phẳng (A'BC) bằng
![]()
![]()
![]()
![]()