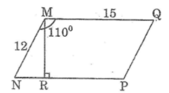
Giả sử hình bình hành \(MNPQ\) có \(MN=12cm,MQ=15cm,\widehat{MNQ}=110^o\)

Ta có \(\widehat{NMQ}+\widehat{MNP}=180^o\) ( hai góc trong cùng phía )
mà \(\widehat{NMQ}=110^o\)

\(\Rightarrow\widehat{MNP}=180^o-110^o=70^o\)

Kẻ \(MR\perp NP\)

Trong tam giác vuông \(MNR\) ta có :
\(MR=MN.sin\widehat{MNP}\)

        \(=12.sin70^o\approx11,276\)

           Vậy \(S_{MNPQ}=MR.MQ\approx11,276.15=169,14\left(cm^2\right)\)

Chúc bạn học tốt !!!

Giả sử ta có hình bình hành ABCD, đường chéo AC, AB=12cm, AC=10cm, `\hat(ABC)=150^o`.

`S_(ABC) = 1/2 . 10. 12 . sinABC = 30 (cm^2)`

Vì đường chéo AC chia hình bình hành ABCD ra 2 tam giác bằng nhau.

`=> S_(ABCD) = 2.S_(ABC) = 60(cm^2)`

`=>` B.

kẻ AH⊥BC; AB=10;BC=12

∠ABC=150

⇒∠ABH=30

xét ΔAHB có ∠H=90

⇒sin B=\(\dfrac{AH}{AB}\)⇒AH=\(\dfrac{1}{2}\).10=5

⇒S_ABCD=AH.AB=5.12=60

⇒chọn B

Diện tích hình binh hành là 90\(\sqrt{3}\) (cm²)

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)

vì ABCD là hình bình hành

=> AD // BC ( tính chất )

=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)

=> \(\widehat{B}=180^0-110^0=70^0\)

Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH

Xét tam giác vuông ABH, có:

AH=AB*sin B=12*sin 70 độ

\(AH\approx11,276\)(cm)

ta có: AD=BC ( ABCD là hình chữ nhật )

\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

A) Vẽ t/g ABC (A là góc nhọn), đường cao BH. 
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)

Gọi hình bình hành đó là ABCD , từ A kẻ đường cao AH xuống cạnh CD (H thuộc CD)

Ta có : \(AH=AD.sinD\)

\(\Rightarrow S_{ABCD}=CD.AH=CD.AD.sinD\)

Vậy ta có điều phải chứng minh

to khong hieu bai nay