Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
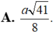
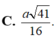
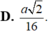
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8 .
B. a 41 24 .
C. a 41 16 .
Đáp án A
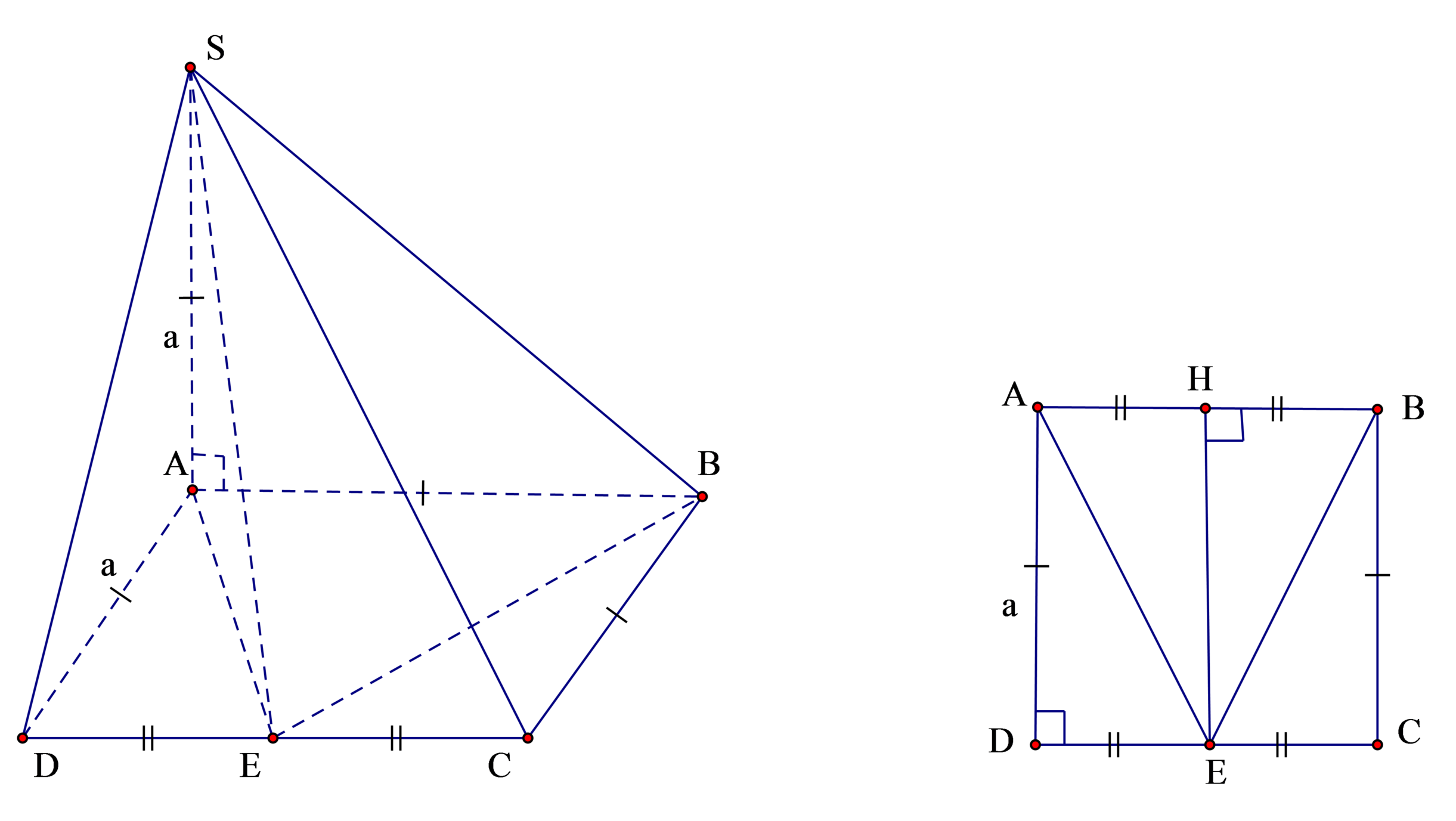
Hình chóp SABE có cạnh bên S A ⊥ đáy (ABE) ta có công thức tính bán kính mặt cầu của hình chóp dạng này là R = R d 2 + h 2 2 ( với R d là bán kính đường tròn ngoại tiếp đáy và h là chiều cao hình chóp )
Ta có: h = S A = a ; d t A B E = 1 2 E H . A B = a 2 2
A E = B E = a 2 + a 2 4 = a 5 2
R d = A B . A E . B E 4 d t A B E = a . 5 a 2 4 4. a 2 2 = a 5 8
vậy R = 25 a 64 2 + a 2 4 = a 41 8 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
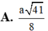
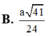
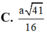
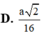
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA = a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8
B. a 41 24
C. a 41 16
D. a 2 16
Đáp án A
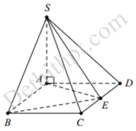
Tam giác ABE cân có A E = B E = a 5 2
và AB = a
⇒ S Δ A B E = a 2 2 = A E . B E . A B 4. R Δ A B E ⇒ R Δ A B E = 2 a . a 5 2 2 : 4 a 2 = 5 a 8
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABE là
R = R Δ A B E 2 + S A 2 4 = 5 a 8 2 + a 2 4 = a 41 8
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh bên SC tạo với đáy góc 60 ο . Thể tích khối chóp S.ABCD là:
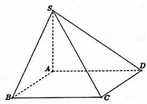
A. a 3 6 3
B. a 3 3 6
C. a 3 6 6
D. a 3 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy ABCD. Góc giữa SC và mặt đáy bằng 45 ° . Gọi E là trung điểm BC. Tính khoảng cách giữa hai đường thẳng DE và SC
A. a 38 19
B. a 5 5
C. a 38 5
D. a 5 19
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, sạnh bên SA vuông góc với mặt đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích khối chóp S.ABCD bằng a 3 3 . Khoảng cách từ điểm A đến mặt phẳng (SBE) bằng
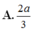
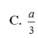
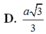
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, sạnh bên SA vuông góc với mặt đáy. Gọi E là trung điểm của cạnh CD. Biết thể tích khối chóp S.ABCD bằng a 3 3 . Khoảng cách từ điểm A đến mặt phẳng (SBE) bằng
A. 2 a 3
B. 2 a 3
C. a 3
D. 3 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy. Góc giữa SC và mặt đáy bằng 45 0 . Gọi E là trung điểm BC. Tính khoảng cách giữa hai đường thẳng DE và SC.
A. a 5 19
B. a 38 19
C. a 5 5
D. a 38 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Gọi E,F lần lượt là hình chiếu của A lên SB,SD. Khẳng định nào sau đây đúng?
A. S C ⊥ A E D
B. S C ⊥ A F B
C. A C ⊥ S B D
D. S C ⊥ A E F
