Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Những câu hỏi liên quan
Có tất cả bao nhiêu cặp số thực (x; y) thỏa mãn đồng thời các điều kiện
3
x
2
-
2
x
-
3
-
log
3
5
5
-...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x; y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - ( y + 4 ) và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Chọn B.
Với 
,
xét từng TH phá dấu trị tuyệt đối, ta tìm được nghiệm
-3 ≤ y ≤ 0
Khi đó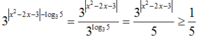 
và 
Do đó
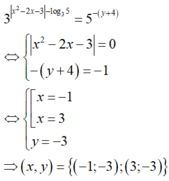
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện
3
x
2
-
2
x
-
3
-
log
3
5
5
-...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - ( y + 4 ) và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện
3
x
2
−
2
x
−
3
−
log
3
5...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x;y) thỏa mãn đồng thời các điều kiện 3 x 2 − 2 x − 3 − log 3 5 = 5 − y + 4 và 4 y − y − 1 + y + 3 2 ≤ 8 ?
A. 3
B. 2
C. 1
D. 4
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện
3
x
2
-
2
x
-
3
-
log
3
5
5...
Đọc tiếp
Có tất cả bao nhiêu cặp số thực (x,y) thỏa mãn đồng thời các điều kiện 3 x 2 - 2 x - 3 - log 3 5 = 5 - y + 4 và 4 y - y - 1 + y + 3 2 ≤ 8 ?
A. 3.
B. 2.
C. 1.
D. 4.
Đáp án B.
Với 4 y - y - 1 + y + 3 2 ≤ 8
xét từng TH phá giá trị tuyệt đối, ta tìm được nghiệm - 3 ≤ y ≤ 0
Khi đó 3 x 2 - 2 x - 3 - log 3 5 = 3 x 2 - 2 x - 3 3 log 3 5 = 3 x 2 - 2 x - 3 5 ≥ 1 5
và y ∈ - 3 ; 0 ⇔ y + 4 ∈ 1 ; 4 ⇒ 5 - y + 4 ≤ 5 - 1 = 1 5
Do đó
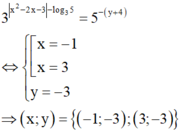
Vậy có tất cả hai cặp số thực (x; y) thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Có tất cả bao biêu bộ ba số thực (x,y,z) thỏa mãn đồng thời các điều kiện dưới đây \(2^{\sqrt[3]{x^2}}.4^{\sqrt[3]{y^2}}.16^{\sqrt[3]{z^2}}=128\) và \(\left(xy^2+z^4\right)^2=4+\left(xy^2-z^4\right)^2\)
Pt đầu tương đương: \(\sqrt[3]{x^2}+2\sqrt[3]{y^2}+4\sqrt[3]{z^2}=7\)
Pt 2 tương đương:
\(\left(xy^2+z^4\right)^2-\left(xy^2-z^4\right)^2=4\)
\(\Leftrightarrow4xy^2z^4=4\)
\(\Leftrightarrow xy^2z^4=1\) (1)
Quay lại pt đầu, áp dụng AM-GM:
\(7=\sqrt[3]{x^2}+\sqrt[3]{y^2}+\sqrt[3]{y^2}+\sqrt[3]{z^2}+\sqrt[3]{z^2}+\sqrt[3]{z^2}+\sqrt[3]{z}\ge7\sqrt[7]{\sqrt[3]{x^2}.\sqrt[3]{y^4}.\sqrt[3]{z^8}}\)
\(\Leftrightarrow\sqrt[21]{x^2y^4z^8}\le1\)
\(\Leftrightarrow x^2y^4z^8\le1\)
\(\Rightarrow\left|xy^2z^4\right|\le1\Rightarrow xy^2z^4\le1\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x^2=y^2=z^2\\xy^2z^4=1\\x>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=\pm1\\z=\pm1\end{matrix}\right.\)
Các bộ thỏa mãn là: \(\left(1;1;1\right);\left(1;1;-1\right);\left(1;-1;1\right);\left(1;-1;-1\right)\)
Đúng 2
Bình luận (2)
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và
log
1
3
5
-
x
log
1
3
3
-
x
? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và log 1 3 5 - x < log 1 3 3 - x ?
A. 1
B. 2
C. 3
D. 4
Chọn B.
Xét bất phương trình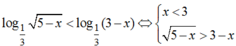 
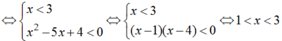
Mặt khác x + 1/3 là số nguyên 
là số nguyên khi 3x + 1 chia hết cho 3.
Ta có 
Vậy có tất cả 2 giá trị của x thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Tìm các cặp số thực (x;y) sao cho x và y thỏa mãn đồng thời hai điều kiện: x=x^2+y^2; y=2xy.
Tìm các cặp số thực(x;y)sao cho x và y thỏa mãn đồng thời hai điều kiện: x=x mũ2+y mũ2 và y=2xy
1) Tìm các số a,b thỏa mãn trong các điều kiện sau:
a + b = | b | - | a |
2) Có bao nhiêu cặp số nguyên (x,y) thỏa mãn một trong các điều kiện sau:
| x | + | y | = 20
| x | + | y | < 20
(Các cặp số (3 ; 4) và (4 ; 3) là hai cặp số khác nhau).