Cho số phức z thỏa mãn = i − m 1 − m m − 2 i , m ∈ ℝ là tham số và z . z ¯ = 1 5 . Khi đó số giá trị thỏa mãn là:
A. 2
B. 1
C. 0
D. 3
Cho số phức z thỏa mãn 1 + i z là số thực và |z-2|=m với m ∈ R. Gọi m 0 là một giá trị của m để có đúng một số phức thỏa mãn bài toán. Khi đó
A. m 0 ∈ ( 0 ; 1 / 2 )
B. m 0 ∈ ( 1 / 2 ; 1 )
C. m 0 ∈ ( 3 / 2 ; 2 )
D. m 0 ∈ ( 1 ; 3 / 2 )
Cho số phức thỏa mãn ( 1 + i ) z + 2 + ( 1 + i ) z - 2 = 4 2 .
Gọi m = m a x z ; n = m i n z và số phức w=m+ni. Tính w 2018 .
A. 4 1009
B. 5 1009
C. 6 1009
D. 2 1009
Đáp án C
Phương pháp
Chia cả 2 vế cho 1 + i và suy ra đường biểu diễn của số phức z
Cách giải
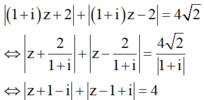
![]() Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4
Tập hợp các điểm z là elip có độ dài trục lớn là 2a=4 ![]() a=2
a=2
và hai tiêu điểm ![]()

Tìm {M} biểu diễn số phức z thỏa mãn |z-i| = |(1+i)z|.
A. {M} là w: x 2 + y + 1 2 = 2
B. {M} là w: x - 1 2 + y 2 = 1
C. {M} là w: x 2 + y + 1 2 = 1
D. {M} là w: x + 1 2 + y 2 = 2
Cho số phức z thỏa mãn z - 2 - 3 i = 1 . Gọi M = m a x z ¯ + 1 + i , m = m i n z ¯ + 1 + i . Tính giá trị của biểu thức M 2 + m 2
A. M 2 + m 2 = 28
B. M 2 + m 2 = 26
C. M 2 + m 2 = 24
D. M 2 + m 2 = 20
Đáp án A.
Ta có 1 = z - 2 - 3 i 2 = z - 2 - 3 i . z - 2 - 3 i ¯ = z - 2 - 3 i z ¯ - 2 + 3 i ¯ = z - 2 - 3 i z ¯ - 2 + 3 i
Lấy môđun hai vế, ta được z - 2 - 3 i . z ¯ - 2 + 3 i = 1 ⇔ z ¯ - 2 + 3 i = 1 ( * )
Đặt w = z ¯ + 1 + i ⇔ z ¯ = w - 1 - i , khi đó (*) ⇔ w - 1 - 2 - 3 i = 1 ⇔ w - 3 + 2 i = 1 .
⇒ w m i n = 3 2 + 2 2 - 1 = 13 - 1 w m i n = 3 2 + 2 2 - 1 = 13 + 1 ⇒ M = 13 + 1 m = 13 - 1 ⇒ M 2 + m 2 = 13 + 1 2 + 13 - 1 2 = 28 .
Tìm {M} biểu diễn số phức z thỏa mãn: z + z ¯ - i = 1 .
A. {M} là {(0,0)}
B. {M} là đường tròn x 2 + y - 1 2 = 0
C. {M}là trục tung
D. {M} là đường thẳng x - y = 1
Cho số phức z thỏa mãn 5 z - i = z + 1 - 3 i + 3 z - 1 + i . Tìm giá trị lớn nhất M của z - 2 + 3 i ?
A. M = 10 3
B. M = 1 + 3
C. M = 4 5
D. M = 9
Cho số phức z thỏa mãn 5 z - i = z + 1 - 3 i + 3 z - 1 + i .
Tìm giá trị lớn nhất M của z - 2 + 3 i
A. M= 10 3
B. M= 1 + 3
C. M= 4 5
D. M= 9
Đáp án C
Gọi ![]() là trung điểm AB
là trung điểm AB
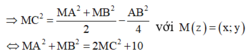
Ta có
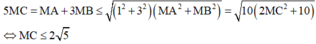
Khi đó
![]()
Cho số phức z thỏa mãn z - 2 + i + z + 1 - i = 13 . Tìm giá trị nhỏ nhất m của biểu thức z - 2 + i
A. m = 1
B. m = 2 13 13
C. m = 13 13
D. m = 1 13
Cho số phức z thỏa mãn z - 2 + i + z + 1 - i = 13 Tìm giá trị nhỏ nhất m của biểu thức z + 2 - i
![]()
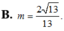

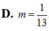
Cho số phức z=x+yi (x,y∈ R) thỏa mãn z+1-2i- z (1-i)=0. Trong mặt phẳng tọa độ Oxy, M là điểm biểu diễn của số phức z, M thuộc đường thẳng nào sau đây?
A. x+y-2=0.
B. x-y+2=0.
C. x+y-1=0.
D. x+y+1=0.