Cho chóp S.ABCD có đáy là hình vuông, S A ⊥ A B C D . Góc giữa đường thẳng SC và mặt phẳng (SAD) là góc?
A. C S A ^
B. C S D ^
C. C D S ^
D. S C D ^
Những câu hỏi liên quan
Trong các phát biểu sau, phát biểu nào đúng?a) Hình chóp đều S.ABCD có đáy là hình bình hành.b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Đọc tiếp
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
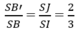
Do đó dễ thấy
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng A.
πa
3
3
B.
2
πa
3
3
C.
πa
3
6
D....
Đọc tiếp
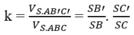
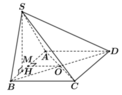
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD bằng
A. πa 3 3
B. 2 πa 3 3
C. πa 3 6
D. 11 11 πa 3 162
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra 
Ta có 
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính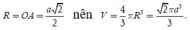 
Chọn B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết ABa, BC2a, BDa
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là
60
0
. Tính thể tích V của khối chóp S.ABCD theo a.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB=a, BC=2a, BD=a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 60 0 . Tính thể tích V của khối chóp S.ABCD theo a.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a A.
V
3
30
a...
Đọc tiếp
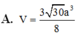
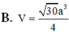
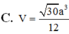
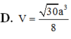
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Đáp án D
Dựng HK ⊥ BD, do SH ⊥ BD nên ta có:
(SKH) ⊥ BD => Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là góc SKH = 600
Lại có: 
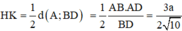
Do đó 
Vậy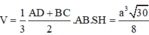 
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB a, BC 2a, BD a
10
. Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a. A. V
3
30
a
3
8
B. V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Chọn D
Ta có 
Gọi H là trung điểm AB thì 
,
kẻ 
, ta có 
là góc giữa (SBD) và (ABCD), do đó 
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD 2a, mặt SAC là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC a
3
. Tính thể tích khối chóp S.ABCD. A.
a
3
3
3
B.
a
3
3...
Đọc tiếp
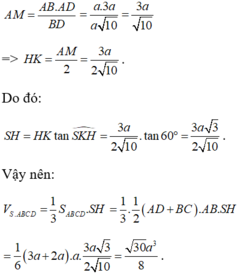
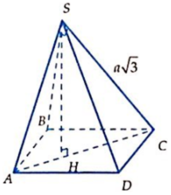
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt SAC là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a 3 . Tính thể tích khối chóp S.ABCD.
A. a 3 3 3
B. a 3 3 4
C. 2 a 3 3 3
D. a 3 3 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a
2
. Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD. A.
2
π
a
3
3
B.
4...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a 2 . Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
A. 2 π a 3 3
B. 4 π a 3 3
C. 2 π a 3 3
D. 4 π a 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a
2
. Tam giác SAC vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình
vuông cạnh a 2 . Tam giác SAC vuông
cân tại S và nằm trong mặt phẳng vuông
góc với đáy. Tính thể tích khối cầu ngoại
tiếp hình chóp S.ABCD.
