Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện z - 1 + i = z + 2 i là đường nào trong các đường cho dưới đây?
A. Đường thẳng
B. Đường tròn
C. Elip
D. Parabo
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: z ¯ + 1 - i ≤ 1
A. Đường tròn tâm I(-1;-1), bán kính R = 1.
B. Hình tròn tâm I(1;-1), bán kính R = 1.
C. Hình tròn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I(1;-1), bán kính R = 1.
Chọn C.
Gọi M(x;y) là điểm biểu diễn của số phức z = x + yi trên mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có :
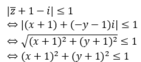
Suy ra, tập hợp các điểm M là hình tròn tâm I(-1;-1) bán kính R = 1 và kể cả đường tròn đó.
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: | z + i | = | z - i | .
A. Trục Oy.
B. Trục Ox.
C. y = x.
D. y = -x.
Chọn B.
Gọi M(x; y) là điểm biểu diễn của số phức z = x + yi trong mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có
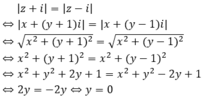
Vậy tập hợp các điểm M là đường thẳng y = 0 hay trục Ox
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: z ¯ + 1 − i ≤ 4
A. Đường tròn tâm I (-1; -1) , bán kính R = 4.
B. Hình tròn tâm I (1; -1), bán kính R = 4.
C. Hình tròn tâm I (-1; -1), bán kính R = 4 (kể cả những điểm nằm trên đường tròn).
D. Đường tròn tâm I (1; -1), bán kính R = 4.
Tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện |z – (1+ i)| = |z + 2i| là đường nào sau đây?
A. Đường thẳng.
B. Đường tròn.
C. Elip.
D. Parabol.
Đường nào dưới đây là tập hợp các các điểm biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện z − i = z + i ?
A. Một đường thẳng
B. Một đường tròn
C. Một đường elip
D. Một đoạn thẳng.
Đáp án A.
Gọi z = x ; y khi đó điều kiện trở thành:
x 2 + y − 1 2 = x 2 + y + 1 2 ⇔ y = − 1
Như vậy quỹ tích là một đường thẳng.
Đường nào dưới đây là tập hợp các các điểm biểu diễn số phức z trong mặt phẳng phức thỏa mãn điều kiện z - i = z + i ?
A. Một đường thẳng
B. Một đường tròn
C. Một đường elip
D. Một đoạn thẳng
Đáp án A.
Gọi
z
=
x
;
y
khi đó điều kiện trở thành ![]() .
.
Như vậy quỹ tích là một đường thẳng
Cho số phức z thỏa mãn điều kiện: z − 1 = z + 3 − 2 i . Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng
B. Đường tròn
C. Một điểm xác định
D. Elip
Đáp án A
Em hãy thực hiện câu này theo cả 2 cách nhé!
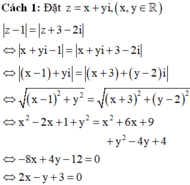
Vậy tập hợp các điểm biểu diễn số phức z là một đường thẳng có phương trình: 2x - y + 3 = 0
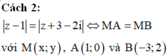
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
AB → = − 4 ; 2 , trung điểm của AB là I − 1 ; 1 , ∆ qua điểm I nhận AB → = − 4 ; 2 làm vectơ pháp tuyến.
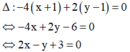
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
A. Đường thẳng.
B. Đường tròn.
C. Một điểm xác định.
D. Elip.
Đáp án A
Em hãy thực hiện Câu nay theo cả 2 cách nhé!
Cách 1: Đặt ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cách 2: ![]() với M(x;y), A(1;0) và B(-3;2)
với M(x;y), A(1;0) và B(-3;2)
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
![]() trung điểm của AB là I(-1;1),
∆
qua điểm I nhận
trung điểm của AB là I(-1;1),
∆
qua điểm I nhận ![]() làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
![]()
![]()
Tìm tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn các điều kiện: |z – i| = 1
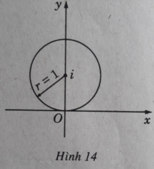
Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z 0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1) (H. 14)
Ta có thể tiến hành như sau:
Cho z = x + iy, ta có | z - 1 | 2 = | x + y - 1 i | 2 = x 2 + y - 1 2 và như vậy ta có: x 2 + y - 1 2 = 1
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.