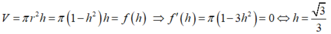Một ống hình trụ rỗng đường kính a được đặt xuyên qua tâm hình cầu bán kính a. Tìm thể tích phần còn lại của hình cầu.
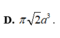
Một ống hình trụ rỗng đường kính a được đặt xuyên qua tâm hình cầu bán kính a. Tìm thể tích phần còn lại của hình cầu.
A. π 3 2 a 3
B. π 3 a 3
C. π 2 3 a 3
D. π 2 a 3
Ta xem hình cầu được sinh bởi khi quay hình tròn (C): x + y = a quanh Oy và hình trụ sinh bởi phần mặt phẳng của hai đường thẳng x = 0; x = a 2 quay quanh Oy.
Ta có y 2 = a 2 - x 2 ⇒ y = ± a 2 - x 2 .
Thể tích cần tìm là:
V = 4 π ∫ a 2 a x a 2 - x 2 dx = - 2 π ∫ a 2 a a 2 - x 2 d a 2 - x 2 = - 4 π 3 a 2 - x 2 3 2 a 2 a = π 3 2 a 3
Đáp án A
Có một khối cầu bằng gỗ bán kính R=10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng một nửa R đối xứng nhau qua tâm khối cầu, một người thợ khoan xuyên tâm khối cầu. Người thợ đã khoan bỏ đi phần hình trụ có trục của nó trùng với trục hình cầu; mặt cắt của hình trụ vuông góc với trục hình trụ là một hình tròn có bán kính bằng 1/2R. Tính thể tích V của phần còn lại của khối cầu (làm tròn đến số thập phân thứ ba).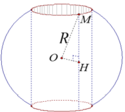
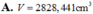
![]()
Có một khối cầu bằng gỗ bán kính R = 10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng 1 2 R đối xứng nhau qua tâm của khối cầu, một người thợ mộc đục xuyên tâm của khối cầu gỗ. Người thợ mộc đã đục bỏ đi phần hình hộp chữ nhật có trục của nó trùng với trục hình cầu và có hai mặt lần lượt nằm trên hai mặt phẳng chứa hai đáy của chỏm cầu; hai mặt này là hai hình vuông có đường chéo bằng R (tham khảo hình vẽ bên).
Tính thể tích V của phần còn lại của khối cầu (làm tròn đến chữ số thập phân thứ ba)

A. V = 3215 , 023 c m 3 .
B. V = 3322 , 765 c m 3 .
C. V = 3268 , 894 c m 3 .
D. V = 3161 , 152 c m 3 .
Đáp án A.
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.
Một cái ống hình trụ tròn xoay bên trong rỗng, có chiều cao bằng 25cm và đường kính đáy bằng 6cm đặt trên cái bàn nằm ngang có mặt bàn phẳng sao cho một miệng ống nằm trên mặt bàn. Người ta đặt lên trên miệng ống còn lại một quả bóng hình cầu có bán kính 5cm. Tính khoảng cách lớn nhất h có thể từ một điểm trên quả bóng tới mặt bàn nếu coi độ dày của thành ống là không đáng kể.
![]()
![]()
![]()
![]()
Cho hình cầu (S) tâm O, bán kính R. Hình cầu (S) ngoại tiếp một hình trụ tròn xoay (T) có đường cao bằng đường kính đáy và hình cầu (S) lại nội tiếp trong một nón tròn xoay (N) có góc ở đỉnh bằng 60 ° . Tính tỉ số thể tích của hình trụ (T) và hình nón (N).
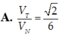
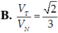
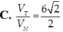
![]()
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a) Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là r cm và chiều cao 2r cm.
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
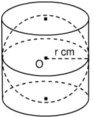
Hình 120
a) Hình cầu bán kính r, vậy thể tích của nó là 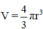
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
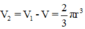
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
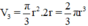
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
![]()
![]()
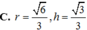
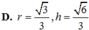
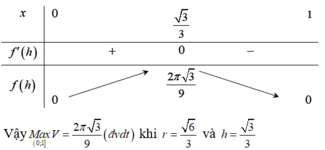
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
A. r = 3 2 ; h = 6 2
B. r = 6 2 ; h = 3 2
C. r = 6 3 ; h = 3 3
D. r = 3 3 ; h = 6 3
Chọn C.
Phương pháp: Dựa vào dữ kiện bài toán lập hàm số và tìm giá trị lớn nhất, nhỏ nhất.

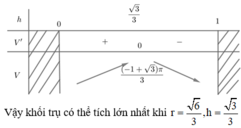
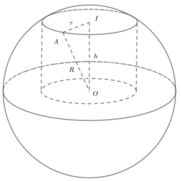
Khi cắt mặt cầu S (O; R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O; R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O; R) để khối trụ có thể tích lớn nhất.
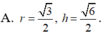


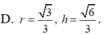
Chọn đáp án C
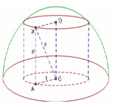
Hình trụ nội tiếp nửa mặt cầu, nên theo giả thiết đường tròn đáy trên có tâm O’ là hình chiếu của O xuống mặt đáy (O’). Suy ra hình trụ và nửa mặt cầu cùng chung trục đối xứng và tâm của đáy dưới hình trụ trùng với tâm O của nửa mặt cầu.
![]()
Thể tích khối trụ là