Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:

( x   -   1 ) 2   +   ( y   +   2 ) 2   +   ( z   +   3 ) 2  = 25

Tìm tọa độ tâm I và bán kính R của mặt cầu (S)

A. I(1; -2; -3); R = 25

B. I(-1; 2; 3); R = 5

C. I(-1; 2; 3); R = 25

D. I(1; -2; -3); R = 5

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x bán kính R=9 có phương trình là

A.  ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 9

B.  ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 81

C.  ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 9

D.  ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 81

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ( x   +   1 ) 2   +   ( y   -   4 ) 2   +   ( z   +   3 ) 2 = 36. Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:

A. 0

B. 1

C. 2

D. Vô số

Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)² + (y+1)² + (z-3)² = 20. Mặt phẳng  có phương trình x-2y+2z-1=0 và đường thẳng  ∆  có phương trình x 1 = y + 2 2 = z + 4 - 30 . Viết phương trình đường thẳng  ∆ ' nằm trong mặt phẳng  α  vuông góc với  ∆  đồng thời cắt (S) theo một dây cung có độ dài lớn nhất.

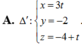
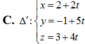
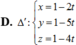
Trong không gian Oxyz, cho mặt cầu (S): x - 1 2 + y + 2 2 + ( z - 5 ) 2 = 9 . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?

A. x – 6y + 8z – 50 = 0

B. x – 2y – 2z – 4 = 0

C. x – 2y – 2z + 4 = 0

D. 3x – 6y + 8z – 54 = 0

Trong không gian Oxyz, cho mặt cầu (S)có phương trình ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 . Tọa độ tâm I và bán kính R của (S) là

A. I(1;2;3)  và  R=5.

B. I(-1;-2;-3)  và R=5. 

C. I(1;2;3)  và R=25.

D. I(-1;-2;-3)  và  R=25

Trong không gian với hệ toạ độ \(Oxyz\), cho mặt cầu \(\left(S\right)\) có phương trình \(x^2+\left(y+1\right)^2+\left(z-2\right)^2=10\) và và đường thẳng \(\Delta\) có phương trình chính tắc là \(\dfrac{x}{2}=\dfrac{y}{-1}=\dfrac{z-1}{2}\). Gọi \(\left(P\right)\) là mặt phẳng thay đổi chứa \(\Delta\). Khi \(\left(P\right)\cap\left(S\right)\) theo đường tròn có bán kính nhỏ nhất, hãy viết phương trình mặt phẳng \(\left(P\right)\) và tính bán kính đường tròn giao tuyến đó.

A. \(\left(P\right):2x-2y+3z+4=0; r=1\)

B. \(\left(P\right):x+y+4z-2=0;r=6\)

C. \(\left(P\right):2x+2y-z+1=0;r=3\)

D. \(\left(P\right):3x-y+2z-1=0;r=4\)

Trong không gian cho Oxyz, mặt cầu (S) có phương trình x 2 + ( y - 4 ) 2 + ( z - 1 ) 2 = 25 . Tâm mặt cầu (S) là điểm

Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 3  và hai đường thẳng d x :   x - 2 1 = y 2 = z - 1 - 1 ;   △ :   x 1 = y 1 = z - 1 - 1 Phương trình nào dưới đây là phương trình mặt phẳng cắt mặt cầu (S) theo giao tuyến là một đường tròn (C) có bán kính bằng 1 và song song với d và △ .

Trong không gian Oxyz, cho mặt cầu (S):

x - 1 2 + y + 2 2 + z - 5 2 = 9  . Phương trình nào dưới đây là phương trình mặt phẳng (P) tiếp xúc với mặt cầu (S) tại điểm A(2;-4;3)?

A. x – 6y + 8z – 50 = 0

B. x – 2y – 2z – 4 = 0

C. x – 2y – 2z + 4 = 0

D. 3x – 6y + 8z – 54 = 0