Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x 3 + ( k 2 - k + 1 ) x trên đoạn [-1;2]. Khi k thay đổi trên ℝ , giá trị nhỏ nhất của M - m bằng.
![]()
![]()
![]()
![]()
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin 2 x − cosx + 3 . Tính giá trị của M + m .
A. 57 8
B. Không tồn tại
C. 41 8
D. 6
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 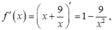
![]()
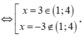
Có ![]()
![]()
Vậy m + M = 16.
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn 1 , 4 . Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x + 9 x trên đoạn [1;4]. Giá trị của m + M bằng
A. 65 4
B. 16
C. 49 4
D. 10
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x + 1 x 2 + x + 1 . Giá trị của M - 3m bằng bao nhiêu?
A. 0
B. 1
C. -1
D. 2
Cho hàm số y = x 4 - 4 x 2 + 3 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn - 1 ; 2 . Giá trị của M + m là
![]()
![]()
![]()
![]()
Cho hàm số y = 3 x − 1 x − 3 . Gọi giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [0;2] lần lượt là M và m. Khi đó m + M có giá trị là
A. 4
B. -14/3
C. 14/3
D. 3/5
Đáp án B
y ' = − 8 x − 3 2 < 0 ; M = f 0 = 1 3 ; m = f 2 = − 5. Vậy M + m = 14 3 .
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x − 4 − x 2 . Tính tổng M + m.
A. M + m = 2 − 2
B. M + m = 2 1 + 2
C. M + m = 2 1 − 2
D. M + m = 4
Chọn C.
Phương pháp:
+) Tìm tập xác định D = [a;b] của hàm số đã cho.

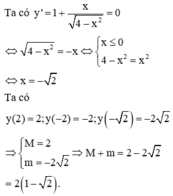
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - 4 - x 2 Tính tổng M+m
A. 2 - 2
B. 2 1 + 2
C. 2 1 - 2
D. 4
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x - 4 - x 2 . Tính tổng M + m.
A. M + m = 2 - 2
B. M + m = 2(1 + 2 )
C. M + m = 2(1 - 2 )
D. M + m = 4
Chọn C
Tập xác định: ![]()
![]()
![]()
Do đó ![]()
Chọn đáp án C