Cho một đa giác đều n đỉnh, n ∈ N , n ⩾ 3 Tìm n biết rằng đa giác đã cho có 27 đường chéo.
![]()
![]()
![]()
![]()
Cho một đa giác đều n đỉnh, nÎN, n≥3. Tìm n biết rằng đa giác đã cho có 27 đường chéo.
A. 12
B. 10
C. 9
D. 16
Chọn C
Với hai đỉnh sẽ cho ta một đoạn thẳng, do đó số đoạn thẳng được tạo ra từ n đỉnh là C n 2
Đa giác có n đỉnh sẽ có n cạnh. Trong số C n 2 đoạn thẳng có n đoạn thẳng là cạnh của đa giác. Do đó số đường chéo của đa giác là
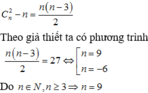
Cho đa giác đều n đỉnh, n ∈ N và n ≥ 3 . Tìm n biết rằng đa giác đã cho có 135 đường chéo
A. n = 15
B. n = 27
C. n = 8
D. n = 18
Đáp án D
Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là C n 2 , trong đó có n cạnh, suy ra số đường chéo là C n 2 - n .
+ Đa giác đã cho có 135 đường chéo nên C n 2 - n = 135 .
+ Giải phương trình
n ! ( n - 2 ) ! 2 ! = 135 ( n ∈ N , n ≥ 2 )
⇔ ( n - 1 ) n - 2 n = 270
⇔ n 2 - 3 n - 270 = 0
<=> n = 18
Cho đa giác đều n đỉnh, n ∈ N và n ≥ 3 Tìm n biết rằng đa giác đã cho có 135 đường chéo.
A. n= 15
B.n = 27
C.n = 8
D.n = 18
Đáp án là D
Đa giác lồi n đỉnh thì có n cạnh.
Nếu vẽ tất cả các đoạn thẳng nối từng cặp trong n đỉnh này thì có một bộ gồm các cạnh và các đường chéo.
Vậy để tính số đường chéo thì lấy tổng số đoạn thẳng dựng được trừ đi số cạnh,
· Tất cả đoạn thẳng dựng được là bằng cách lấy ra 2 điểm bất kỳ trong n điểm, tức là số đoạn thẳng chính là số tổ hợp chập 2 của n phần tử.
Như vậy, tổng số đoạn thẳng là C n 2
· Số cạnh của đa giác lồi là n
Suy ra số đường chéo của đa giác đều n đỉnh là:
C n 2 - n = n ! ( n - 2 ) ! . 2 ! - n = n . ( n - 1 ) 2 - n = n ( n - 3 ) 2
Theo bài ra, ta có n ≥ 3 n ( n - 3 ) 2 = 135 ⇔ n ≥ 3 n 2 - 3 n - 270 = 0 ⇔ n = 18
Cho đa giác đều n đỉnh, n ∈ N v à n ≥ 3 . Tìm n biết rằng đa giác đã cho có 135 đường chéo
A. n = 15
B. n = 27
C. n = 8
D. n = 18
Đáp án D
Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là C n 2 , trong đó có n cạnh, suy ra số đường chéo là C n 2 - n
+ Đa giác đã cho có 135 đường chéo nên C n 2 − n = 135
+ Giải phương trình
n ! n − 2 ! 2 ! = 135 , n ∈ ℕ , n ≥ 2 ⇔ n − 1 n − 2 n = 270 ⇔ n 2 − 3 n − 270 = 0 ⇔ n = 18 n h a n n = − 15 l o a i ⇔ n = 18
Cho đa giác đều n đỉnh, n ∈ ℝ và n > 3. Tìm n biết rằng đa giác đã cho có 135 đường chéo.
A. n = 15
B. n = 8
C. n = 18
D. n = 27
Chọn C.
Phương pháp:
Số đường chéo của đa giác có n đỉnh
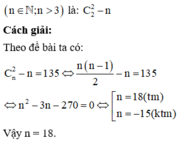
cho đa giác đều n đỉnh tìm n biết răng đa giác có 135 đường chéo
Cho đa giác lồi n đỉnh. Biết rằng số hiệu số đường chéo của đa giác và số cạnh là 25. Tìm n.
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là 3 29 . Tìm n?
A. 20
B. 12
C. 15
D. 10
Cho H là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O n ∈ N , n ≥ 2 . Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác H . Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1 3. Tìm n.