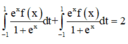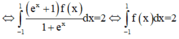Cho là hàm số f(x) liên tục trên R. Biết ∫ 1 e 3 f ln x x d x = 5 , ∫ 0 0,5 n f sin x . cos x d x = 2 . Tính ∫ 1 3 f x d x .
A. 7.
B. 3
C. -3.
D. 10
Cho hàm số y = f(x) liên tục trên khoảng 0 ; + ∞ . Biết f(1) = 1 và f(x) = xf'(x) + ln (x). Giá trị f(e) bằng
A. e
B. 1
C. 2
D. 1 e
Cho hàm số y = f ( x ) liên tục trên 0 ; + ∞ .
Biết f ' ( x ) ln ( x ) x v à f ( 1 ) = 3 2 và tính f ( 3 )
![]()
![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).
A. 4 e 2 - 4 e + 4
B. 4 e 2 - 2 e + 1
C. 2 e 3 - 2 e + 2
D. 4 e 2 + 4 e - 4
Cho hàm số f(x) liên tục trên R+ và thoả mãn ∫ f ( x + 1 ) x + 1 d x = 2 ( x + 1 + 3 ) x + 5 + C . Nguyên hàm của hàm số f(2x) trên tập R+ là
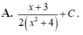
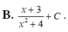
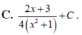
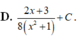
Cho hàm số f(x) liên tục trên R. Biết x.ex là 1 nguyên hàm của f(x).e2x, tìm họ tất cả nguyên hàm của hàm số f'(x).e2x
Từ giả thiết: \(\int f\left(x\right).e^{2x}dx=x.e^x+C\)
Đạo hàm 2 vế:
\(\Rightarrow f\left(x\right).e^{2x}=e^x+x.e^x\)
\(\Rightarrow f\left(x\right)=\dfrac{e^x+x.e^x}{e^{2x}}=\dfrac{x+1}{e^x}\)
Xét \(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2.e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=f\left(x\right).e^{2x}-2\int f\left(x\right).e^{2x}dx=\left(\dfrac{x+1}{e^x}\right)e^{2x}-2.x.e^x+C\)
\(=\left(1-x\right)e^x+C\)
Cho hàm số f(x) liên tục và có đạo hàm trên R và f ' ( x ) = e - f ( x ) ( 2 x + 3 ) ; f ( 0 ) = ln 2 . Tính ∫ 1 2 f ( x ) dx ?
A. 6ln2 + 2.
B. 6ln2 – 2.
C. 6ln2 – 3.
D. 6ln2 + 3.
Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x), biết ∫ 0 9 f x d x = 9 và F(0) = 9.
A. F(9) = -3
B. F(9) = -12.
C. F(9) = 12.
D. F(9) = 6.
Cho hàm số f(x) liên tục trên R và F(x) là một nguyên hàm của f(x) biết ∫ 0 9 f x d x = 9 và F(0)=9
A. F(9) = -3
B. F(9) = -12
C. F(9) = 12
D. F(9) = 6
Cho hàm số y= f(x) liên tục trên R. Biết ∫ 0 x 2 f ( t ) dt = e x 2 + x 4 - 1 với ∀x∈R. Giá trị của f(4) là
A. f ( 4 ) = e 4 + 4 .
B. f ( 4 ) = e 4
C. f ( 4 ) = e 4 + 8 .
D. f(4)=1
Cho hàm số y = f(x) liên tục trên R và là hàm số chẵn, biết ∫ - 1 1 f ( x ) 1 + e x d x = 1 . Tính ∫ - 1 1 f ( x ) d x
A. 1
B. 2
C. 4
D. 1/2
Đáp án B
Phương pháp: Đặt t = - x
Cách giải: I = ∫ - 1 1 f ( x ) 1 + e x d x = 1 (1)
Đặt t = - x => dt = - dx
Đổi cận 
Khi đó:
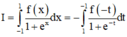
 (do là hàm chẵn)
(do là hàm chẵn)
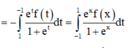
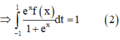
Từ (1), (2), suy ra