Một hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc B A D ⏜ = 60 ∘ , cạnh bên hợp với đáy góc 45 ∘ sao cho A’ chiếu xuống mặt phẳng (ABCD) trùng với giao điểm O của hai đường chéo mặt đáy. Tính thể tích hình hộp.
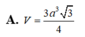
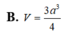
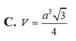
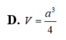
Một hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc B A D ^ = 60 o , cạnh bên hợp với đáy góc 45 o sao cho A’ chiếu xuống mặt phẳng ( ABCD ) trùng với giao điểm O của hai đường chéo mặt đáy. Tính thể tích hình hộp.
A. V = 3 a 3 3 4
B. V = 3 a 3 4
C. V = a 3 3 4
D. V = a 3 4
S A B C D = 2 . a 2 3 4 = a 2 3 2
∆ A A ' O vuông cân ⇒ A ' O = A O = a 3 2
Vậy: V = a 2 3 3 . a 3 3 = 3 a 3 4
Đáp án B
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a 3 . Hình chiếu vuông góc với B' trên mặt phẳng (ABCD) là trung điểm AC, mặt phẳng (CDD'C') tạo với đáy góc 60 0 .Tính theo a thể tích khối hộp ABCD.A'B'C'D'
A . 9 a 3 8
B . a 3 8
C . 27 a 3 8
D . 2 a 3 3 9
Đáp án C.
Chú ý
∆
ABC đều cạnh
a
3
. Kẻ OH
⊥
AB ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cho hình hộp đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 ° , AB' hợp với đáy một góc 30 ° . Thể tích của khối hộp là
A. a 3 2
B. 3 a 3 2
C. a 3 6
D. a 3 2 6
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , A B ' hợp với đáy (ABCD) một góc 30 ° . Thể tích của khối hộp là
A. a 3 2 .
B. 3 a 3 2 .
C. a 3 6 .
D. a 3 2 6 .
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a và B A D ^ = 60 0 , AB' hợp với đáy (ABCD) một góc 30 0 . Thể tích của khối hộp là
A. a 3 2
B. 3 a 3 2
C. a 3 6
D. a 3 2 6
Đáp án C
B D = a ⇒ B O = a 2 ⇒ A O = a 2 - a 2 4 = a 3 2 ⇒ A C = a 3 A ' A , A B C D = A ' A , A ' B ' = A B ' A ' ⇒ A A ' = A ' B ' . tan 30 0 = a 3 3 ⇒ V = 1 3 a 3 3 1 2 a 3 . a = a 3 6
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, góc BCD= 120 o và AA'= Hình chiếu vuông góc của A' lên mặt phẳng ABCD trùng với giao điểm của AC và BD.
Tính theo a thể thích khối hộp ABCD.A'B'C'D'

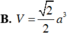
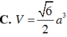
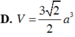
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O, cạnh a, B'D' = a 2 . Góc giữa CC' và mặt đáy là 60 0 , trung điểm H của AO là hình chiếu vuông góc của A' lên (ABCD). Thể tích của hình hộp là:
A. 3 a 3 8
B. a 3 3 8
C. 3 a 3 4
D. a 3 8
Phương pháp:
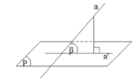
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
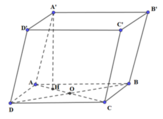
∆ AOD vuông tại O
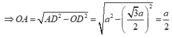
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Thể tích khối hộp là: 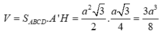
Chọn: A
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O, cạnh a, B ' D ' = a 3 . Góc giữa CC' và mặt đáy là 60 ° , trung điểm H của AO là hình chiếu vuông góc của A' lên (ABCD). Thể tích của hình hộp là:
A. 3 a 3 8
B. a 3 3 8
C. 3 a 3 4
D. a 3 8
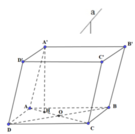
∆ A O D vuông tại O
⇒ O A = A D 2 - O D 2 = a 2 - 3 a 2 2 = a 2 ⇒ A H = 1 2 A O = a 4 ;
AC=2.AO=a và S A B C D = 1 2 . A C . B D
= 1 2 a . a . 3 = a 2 3 2
Do AA'//CC' nên
∠ ( A A ' ; ( A B C D ) ) = ∠ ( C C ' ; A B C D ) = 60 °
Do
A H ⊥ ( A B C D ) ⇒ ∠ ( A A ' ; ( A B C D ) ) = ∠ ( A A ' ; A H ) = ∠ A ' A H = 60 °
∆ A ' A H vuông tại
H ⇒ A ' H = A H . tan A ' A H = a 4 . tan 60 ° = a 3 4
Thể tích khối hộp là V = S A B C D . A ' H
= a 2 3 2 . a 3 4 = 3 a 3 8
Chọn đáp án A.
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O, cạnh a, B'D' = a 3 . Góc giữa CC ' và mặt đáy là 60 ° , trung điểm H của AO là hình chiếu vuông góc của A ' lên (ABCD). Thể tích của hình hộp là
A. 3 a 2 8
B. a 3 3 8
C. 3 a 3 4
D. a 3 8