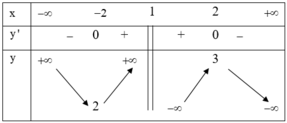
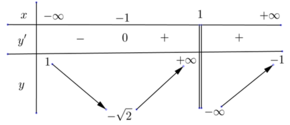
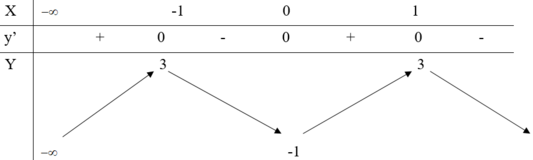
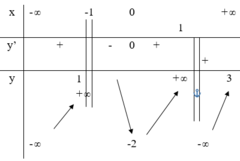
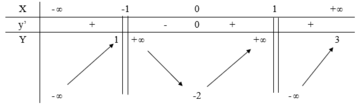
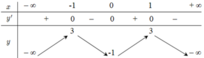
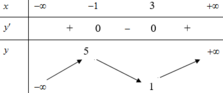
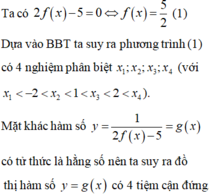Cho hàm số y = f(x) liên tục trên ℝ \{1} và có bảng biến thiên như sau:
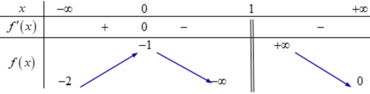 Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
A. 1
B. 2
C. 0
D. 2