Gọi S là tập hợp tất cả các nghiệm của phương trình
3 π 6 - x + tan x . tan π 6 - x + 3 tan x = tan 2 x trên đoạn 0 ; 10 π Số phần tử của S là:
A. 19
B. 20
C. 21
D. 22
Cho phương trình sin x 1 + cos x = 0. Gọi T là tập hợp tất cả các nghiệm của phương trình trên đoạn [0;2018 π ]. Tìm số phần tử của tập T.
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 = m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
Đáp án C.
Đặt t = sin x , t ∈ − 1 ; 1 . Phương trình đã cho trở thành 2 t + 1 t + 2 = m (*).
Để phương trình đã cho có đúng hai nghiệm thuộc đoạn 0 ; π thì phương trình (*) phải có đúng một nghiệm thuộc nửa khoảng 0 ; 1 .
Xét hàm số f t = 2 t + 1 t + 2 . Ta có f ' t = 3 t + 2 2 .
Bảng biến thiên của :
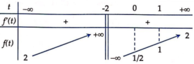
Vậy để phương trình (*) có đúng một nghiệm thuộc nửa khoảng 0 ; 1 thì m ∈ 1 2 ; 1 . Vậy C là đáp án đúng
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình 2 sin x + 1 sin x + 2 =m có đúng hai nghiệm thuộc đoạn 0 ; π . Khi đó S là
A. một khoảng
B. một đoạn
C. một nửa khoảng
D. một tập hợp có hai phần tử
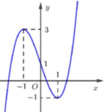
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ dưới. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình f(sin x) = 2sin x +m có nghiệm thuộc khoảng 0 ; π . Tổng các phần tử của S bằng:
A. -10
B. -8
C. -6
D. -5
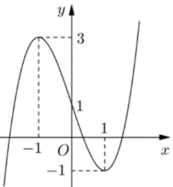
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Gọi S là tập hợp tất cả các số nguyên m để phương trình f(sinx)=3sinx+m có nghiệm thuộc khoảng 0 ; π Tổng các phần tử của S bằng
A. -5
B. -8
C. -6
D. -10
Đặt ![]() khi đó yêu cầu bài toán trở thành phương trình
khi đó yêu cầu bài toán trở thành phương trình
![]() có nghiệm
t
∈
(
0
;
1
]
Có
có nghiệm
t
∈
(
0
;
1
]
Có
![]()
Do đó
![]()
![]()
![]()
Vậy ![]()
Tổng các phần tử của tập S bằng -10.
Chọn đáp án D.
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan π 6 - x + tan x . tan π 6 - x + 3 . tan x = tan 2 x trên đoạn 0 ; 10 π . Số phần tử của S là.
A. 19
B. 20
C. 21
D. 22
Chọn B.
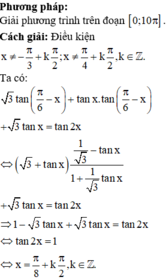
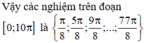
Vậy có 20 nghiệm thỏa mãn yêu cầu bài toán.
Gọi S là tập hợp các giá trị thực của tham số m sao cho phương trình ( x + 1 ) 3 + 3 - m = 3 3 x + m 3 có đúng nghiệm thực. Tích tất cả các phần tử của tập hợp S là
A. -1
B. 1
C. 3
D. 5
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan( π 6 - x) + tanx.tan( π 6 - x) + 3 tanx = tan2x trên đoạn [0;10π]. Số phần tử của S là:
A. 19
B. 20
C. 21
D. 22
Đáp án B
Phương pháp: Sử dụng công thức 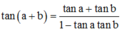
Cách giải:
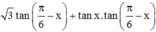
![]()
![]()
![]()
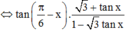
![]()
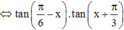
![]()
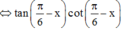
![]()
![]()
![]()
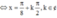
![]()
![]()
![]()
![]()
Ứng với mỗi giá trị của k ta có 1 nghiệm x.
Vậy số phần tử của S là 20.
Gọi S là tập hợp tất cả giá trị nguyên dương và nhỏ hơn 9 của m để bất phương trình x2 + 6x <= 2m( |x + 3| - 2 ) - 6 có nghiệm thực. Tính tổng tất cả các phần tử của S
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan π 6 - x + tan x . tan π 6 - x + 3 tan x = tan 2 x trên đoạn 0 ; 10 π . Số phần tử của S là
A. 19
B. 20
C. 21
D. 22