Tất cả các nghiệm của phương trình tan x + 3 . c o t x - 3 - 1 = 0 là

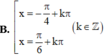
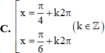
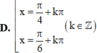
Tất cả các nghiệm của phương trình tan x = c o t x là
A. x = π 4 + k π 4 , k ∈ ℤ
B. x = π 4 + k 2 π , k ∈ ℤ
C. x = π 4 + k π , k ∈ ℤ
D. x = π 4 + k π 2 , k ∈ ℤ
Tìm tất cả các nghiệm của phương trình tan x = m ( m ∈ ℝ )
![]()
![]()
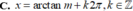
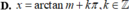
Phương trình tan x = cot x có tất cả các nghiệm là:
![]()
![]()
![]()
![]()
Tính tổng tất cả các nghiệm của phương trình e sin x - π 4 = tan x thuộc đoạn 0 ; 50 π ?
A. 1853 π 2
B. 2475 π 2
C. 2671 π 2
D. 2105 π 2
Đáp án B
Điều kiện: tan x > 0
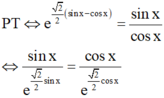
Xét hàm số y = f t = t e 2 2 t t ∈ - 1 ; 1
Khi đó f ' t = e 2 2 1 - t 2 2 e 2 t > 0 ∀ t ∈ - 1 ; 1
do đó hàm số f(t) đồng biến trên [–1;1]
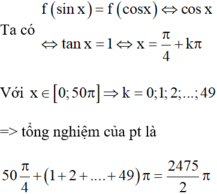
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan π 6 - x + tan x . tan π 6 - x + 3 . tan x = tan 2 x trên đoạn 0 ; 10 π . Số phần tử của S là.
A. 19
B. 20
C. 21
D. 22
Chọn B.
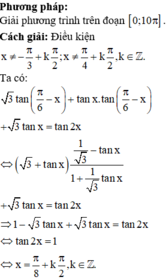
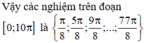
Vậy có 20 nghiệm thỏa mãn yêu cầu bài toán.
Gọi S là tập hợp tất cả các nghiệm của phương trình 3 tan( π 6 - x) + tanx.tan( π 6 - x) + 3 tanx = tan2x trên đoạn [0;10π]. Số phần tử của S là:
A. 19
B. 20
C. 21
D. 22
Đáp án B
Phương pháp: Sử dụng công thức 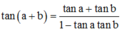
Cách giải:
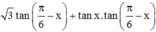
![]()
![]()
![]()
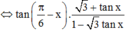
![]()
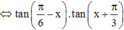
![]()
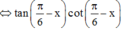
![]()
![]()
![]()
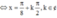
![]()
![]()
![]()
![]()
Ứng với mỗi giá trị của k ta có 1 nghiệm x.
Vậy số phần tử của S là 20.
Tính tổng T tất cả các nghiệm của phương trình
( x - 3 ) 2 x 2 - 5 x = 1 .
A. T = 0
B. T = 4
C. T = 13 2
D. T = 15 2
Ta xét các trường hợp sau:
+ TH1. x- 3= 1 hay x= 4. Khi đó; phương trình đã cho trở thành : 112= 1 luôn đúng.
=> x= 4 là nghiệm của phương trình.
+ TH2. .
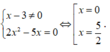
Vậy phương trình đã cho có ba nghiệm
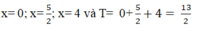
Chọn C.
Tính tổng T tất cả các nghiệm của phương trình log 5 25 - 5 x + x - 3 = 0 .
A.1
B.3
C.25
D.2
Gọi S là tập hợp tất cả các nghiệm của phương trình
3 π 6 - x + tan x . tan π 6 - x + 3 tan x = tan 2 x trên đoạn 0 ; 10 π Số phần tử của S là:
A. 19
B. 20
C. 21
D. 22
Đáp án B
Phương pháp: Sử dụng công thức 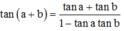
Cách giải:
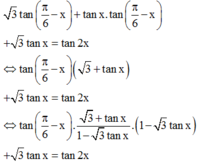
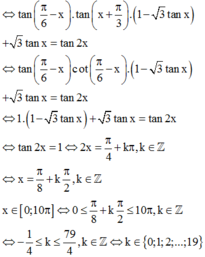
Ứng với mỗi giá trị của k ta có 1 nghiệm x.
Vậy số phần tử của S là 20.