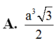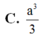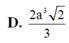Cho khối chóp S . A B C D có đáy là hình chữ nhật cạnh A D = 2 a , A D = a Hình chiếu của đỉnh S lên đáy là trung điểm của cạnh AB cạnh bên SC tạo với mặt phẳng đáy một góc 45 0 Tính thể tích V của khối chóp đã cho.
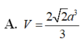
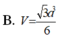
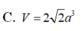
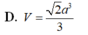
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật cạnh a, S A ⊥ (A B C D) ,SC tạo với mặt đáy một góc 60 độ và (SAB ) một góc a với sin a = căn 3/ 4 . Tính chiều cao khối chóp.
Đáy là hình vuông hay chữ nhật bạn? Hình chữ nhật sao có các cạnh bằng nhau và bằng a được?
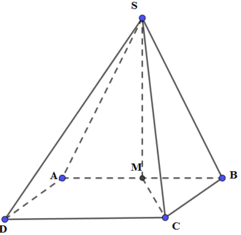
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Chọn C
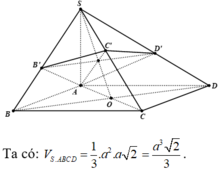
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
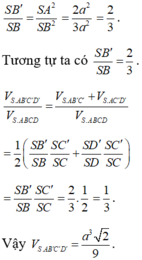

Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của đỉnh S lên đáy là trung điểm của AB, cạnh bên SC tạo với đáy một góc 450. Tính thể tích V của khối chóp đã cho.
A. V = 2 2 a 3 3
B. V = 3 a 3 6
C. V = 2 2 a 3
D. V = 2 a 3 3
Đáp án A
Phương pháp:
+) Xác định góc giữa SC và mặt đáy là góc giữa SC và hình chiếu của nó trên (ABCD).
+) Áp dụng định lí Pytago tính SM.
![]()
Cách giải:
Gọi M là trung điểm của AB ⇒ SM ⊥ (ABCD)

Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của đỉnh S lên đáy là trung điểm của AB, cạnh bên SC tạo với đáy một góc 450. Tính thể tích V của khối chóp đã cho.
Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB = 2a, AD = a. Hình chiếu của đỉnh S lên đáy là trung điểm của cạnh AB cạnh bên SC tạo với mặt phẳng đáy một góc 45 ° Tính thể tích V của khối chóp đã cho.
A. V = 2 2 a 3 3
B. V = 3 a 3 6
C. V = 2 2 a 3
D. V = 2 a 3 3
Cho khối chóp S.ABCDS.ABCD có đáy là hình chữ nhật, AB=2a,AD=2\sqrt{3}a,SAAB=2a,AD=23a,SA vuông góc với đáy và mặt phẳng (SBC)(SBC) tạo với đáy một góc 60^o60o. Thể tích khối chóp S.ABCDS.ABCD bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. AB=a, BC=2a cạnh bên SA vuông góc với đáy và SA=a 2 Tính thể tích khối chóp S.ABCD
A. 2 3 a 3 3
B. 2 2 a 3 3
C. 2 2 a 3
D. 2 a 3
Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = a 3 , SA ⊥ (ABCD), SC tạo với đáy một góc 450 . Gọi M là trung điểm của SB , N là điểm trên cạnh SC sao cho
SN = 1 2 NC . Tính thể tích khối chóp S . AMN
A. a 3 3 9
B. a 3 3 18
C. a 3 3 12
D. a 3 3 6
Phương pháp:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
(Công thức Simson): Cho khối chóp S.ABC, các điểm A1, B1, C1 lần lượt
thuộc SA, SB, SC. Khi đó,
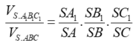
Cách giải:
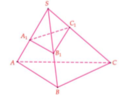
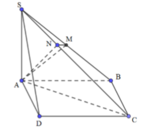
ABCD là hình chữ nhật ![]()
Ta có:
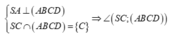
![]()
![]()
Thể tích khối chóp S.ABCD là:
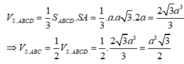
Ta có: 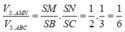
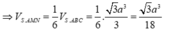
Chọn: B
Chú ý: Công thức tỉ số thể tích trên chỉ áp dụng cho chóp tam giác.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=2a, AD=a. Hình chiếu của S lên đáy là trung điểm H của cạnh AB, góc tạo bởi SC và đáy bằng 45 0 . Tính thể tích khối chóp S.ABCD