Mặt cầu (S) có diện tích bằng 100 π ( cm 2 ) thì có bán kính là:
A. 3 (cm)
![]()
![]()
![]()
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng
A. 3 2
B. 3
C. 1 2
D. 1
Chọn C.
Phương pháp:
Công thức tính diện tích mặt cầu bán kính R là: S = 4 π R 2 .
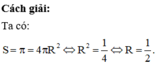
Một mặt cầu có diện tích xung quanh là π thì có bán kính bằng:
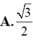
![]()
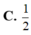
![]()
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h
a) Khi r = 12 (cm) và thể tích hai hình bằng nhau thì giá trị h(cm) làm tròn đến chữ số thập phân thứ nhất là bao nhiêu ?
b) Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích "hình tròn đáy" gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu ?
a) Giá trị gần đúng của h là : 10,5 cm
b) Giá trị của r là : 24 cm
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:
a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8 c m 3
a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h. Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?

Theo đề bài, tổng diện tích nửa mặt cầu và diện tích hình tròn đáy gấp 3 lần diện tích toàn phần của hình trụ nên:
![]()
Diện tích mặt cầu có bán kính R = 2(cm) là:
A. 8π ( c m 2 )
B. 16π ( c m 2 )
C. 32π ( c m 2 )
D. 64π ( c m 2 )
Cho hai hình cầu A và B lần lượt có bán kính là 3 cm và 6 cm. So sánh diện tích hai mặt cầu của hai hình cầu đó là:
A. S A = S B
B. S A = 2 S B
C. S A = 1 2 S B
D. S A = 1 4 S B
Mặt cầu (S) có diện tích bằng 100 π c m 2 thì có bán kính là
A. 3
B. 5
C. 4
D. 5
Mặt cầu (S) có diện tích bằng 100 π c m 2 thì có bán kính là
A. 3 c m
B. 5 c m
C. 4 c m
D. 5 c m