Cho hai đường thẳng d: x = 1 - t y = 2 + 2 t z = 3 t và d: x = 1 + t y = 3 - 2 t z = 1 chứng minh d và d' chéo nhau.

Những câu hỏi liên quan
Cho các đường thẳng (d): y = 2x + 5m - 1 và đường thẳng (t): y = 4 - 3x. Tìm m để hai đường thẳng cắt nhau tại điểm A(x; y) có tọa độ thỏa mãn: x - 2y < 6
Tọa độ giao điểm là:
2x+5m-1=4-3x và y=4-3x
=>5x=4+1-5m và y=-3x+4
=>x=-m+1 và y=-3*(-m+1)+4=3m-3+4=3m+1
x-2y<6
=>-m+1-6m-3<6
=>-7m-2<6
=>-7m<8
=>m>-8/7
Đúng 0
Bình luận (0)
Trong mặt phẳng $O x y$, cho hai đường thẳng $(d): y=m x+3 ~m+2$ và $\left(d_{1}\right): y=x+1$. Tìm giá trị của $m$ để hai đường thẳng $(d)$ và $\left(d_{1}\right)$ song song với nhau.
Cho hai đường thẳng d và d'. Tìm m để góc giữa hai đường thẳng đó bằng 90°, với:
d: (m+3)x- (m-1)y+m-3=0
d': (m-2)x+ (m+1)y - m-1=0
Cho hai đường thẳng x + y = -1 (d1) và mx + y = 1 (d2). Tìm m để hai đường thẳng (d1) và (d2) cắt nhau tại một điểm thuộc trục hoành
Lời giải:
Do $(d_1),(d_2)$ cắt nhau tại trục hoành nên tung độ bằng $0$. Gọi giao điểm của $(d_1); (d_2)$ là $(a,0)$. Ta có:
\(\left\{\begin{matrix} a+0=-1\\ ma+0=1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=-1\\ ma=1\end{matrix}\right.\Rightarrow m(-1)=1\Rightarrow m=-1\)
Vậy.........
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
v
à
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 v à ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng ∆1;∆2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Chọn A.
Gọi ∆ là đường thẳng cần tìm
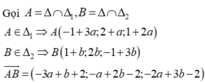
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
![]()
![]()
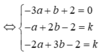
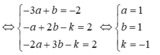
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương ![]()
Vậy phương trình của ∆ là
Đúng 0
Bình luận (0)
Cho hai đường thẳng d và d'. Tìm m để hai đường thẳng: cắt nhau, song song, đồng quy
a) d: 2mx+(m-1).y-2=0, d': (m+2).x+(2m+1).y-(m+2)=0
b) d: (m-2).x+(m-6).y+m-1=0, d': (m-4).x+(2m-3).y+m-5=0
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
và
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Chọn A.
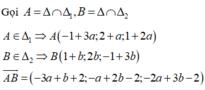
![]()

Ta có A(2;3;3); B(2;2;2)
Δ đi qua điểm A(2;3;3) và có vectơ chỉ phương A B → = 0 ; - 1 ; 1
Vậy phương trình của ∆ là x = 2 y = 3 - t z = 3 - t
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
∆
1
:
x
+
1
3
y
-
2
1
z
-
1
2
và
∆
2
:
x
-
1
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng ∆ 1 : x + 1 3 = y - 2 1 = z - 1 2 và ∆ 2 : x - 1 1 = y 2 = z + 1 3 . Phương trình đường thẳng ∆ song song với d : x = 3 y = - 1 + t z = 4 + t và cắt hai đường thẳng Δ1; Δ2 là:
A. x = 2 y = 3 - t z = 3 - t
B. x = - 2 y = - 3 - t z = - 3 - t
C. x = - 2 y = - 3 + t z = - 3 + t
D. x = 2 y = - 3 + t z = 3 + t
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
2
-
1
y
-
1
3
z
-
1
2
và
d
2
:
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 2 - 1 = y - 1 3 = z - 1 2 và d 2 : x = 1 - 3 t y = - 2 + t z = - 1 - t . Phương trình đường thẳng d nằm trong ( α ) : x + 2 y - 3 z - 2 = 0 và cắt hai đường thẳng d1; d2 là:
A. x + 3 5 = y - 2 - 1 = z - 1 1
B. x + 3 - 5 = y - 2 1 = z - 1 - 1
C. x - 3 - 5 = y + 2 1 = z + 1 - 1
D. x + 8 1 = y - 3 3 = z - 4
Chọn C.
*) Gọi A = d1 ∩ (α)
A ∈ d1 ⇒ A(2-a;1+3a;1+2a)
Mà điểm A thuộc mp(α) nên thay tọa độ điểm A vào phương trình mặt phẳng ta được
(2 - a) + 2(1 + 3a) – 3(1 + 2a) – 2= 0
2 – a + 2 + 6a – 3 – 6a – 2 = 0
⇒ a = -1 ⇒ A(3;-2;-1)
*) Gọi B = d2 ∩ (α)
B ∈ d2 ⇒ B(1-3b;-2+b;-1-b)
Mà điểm B thuộc mp(α) nên thay tọa độ điểm B vào phương trình mặt phẳng ta được:
(1 - 3b) + 2(-2 + b) - 3(-1 - b) - 2 = 0
1- 3b – 4 + 2b + 3 + 3b - 2 = 0
⇔ 2b - 2 = 0 ⇔ b = 1 ⇒ B(-2;-1;-2)
*) Đường thẳng d đi qua điểm A(3;-2;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 3 - 5 = y + 2 1 = z + 1 - 1
Đúng 0
Bình luận (0)
Cho các đường thẳng d1: x+y+3=0 , d2: x-y-4=0 , d3: x-2y=0. Tìm tọa độ điểm M nằm trên đường thẳng d3 sao cho khoảng cách từ M đến đường thẳng d1 bằng hai lần khoảng cách từ M đến đường thẳng d2
Do \(M\in d_3\) \(\Rightarrow M\left(2a;a\right)\)
\(\frac{\left|2a+a+3\right|}{\sqrt{1^2+1^2}}=2\frac{\left|2a-a-4\right|}{\sqrt{1^2+\left(-1\right)^2}}\Leftrightarrow\left|3a+3\right|=2\left|a-4\right|\)
\(\Leftrightarrow\left(3a+3\right)^2=4\left(a-4\right)^2\Leftrightarrow9a^2+18a+9=4a^2-32a+64\)
\(\Leftrightarrow5a^2+50a-55=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-11\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(-22;-11\right)\end{matrix}\right.\)
Đúng 0
Bình luận (1)












