Phương trình z 2 + 1 = 2 2 i có các nghiệm là z 1 , z 2 . Tính T = | z 1 | + | z 2 |
A. 2
B. 2 2
C. 2 3
D. 12
Phương trình z 1 = 1 + 2 i , z 2 = 2 - 3 i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Chọn D
Thay z = 2 + i vào phương trình đã cho ta có:
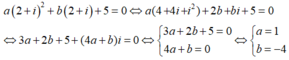
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Phương trình ( 1 + i ) 2 = - 7 + i có các nghiệm là
A. -1 - 2i và 1 + 2i
B. -1 + 2i và 1 + 2i
C. -1 + 2i và 1 - 2i
D. 1 + 2i và 1 - 2i
Câu 1 :Chứng minh phương trình 11x^2+5=y^2 có vô số nghiệm nguyên có dạng y=11z-4; z thuộc Z
Câu 2 : Chưng minh phương trình: 7x^2+2= y^2 có vô số nghiệm nguyên.
Câu 3 : Tìm các số nguyên thoả mãn: 8x^2y^2 +x^2+y^2=10xy
MÌNH ĐANG CẦN GẤP GIẢI GIÚP MÌNH NHA !
Phương trình z 2 - z + 1 = 0 có hai nghiệm là
A. 1 ± 3 i 2
B. - 1 ± 3 i 2
C. 1 ± 3 i
D. - 1 ± 3 i
Gọi z1 z2 là hai nghiệm phức của phương trình \(z^2-4z+5=0\) . Tính:
w = \(\dfrac{1}{z_1}+\dfrac{1}{z_2}+i\left(z_1^2z_2+z^2_2z_1\right)\)
\(z^2-4z+5=0\Rightarrow\left\{{}\begin{matrix}z_1+z_2=4\\z_1z_2=5\end{matrix}\right.\) theo hệ thức Viet
\(w=\dfrac{z_1+z_2}{z_1z_2}+i.z_1z_2\left(z_1+z_2\right)=\dfrac{4}{5}+i.5.4=\dfrac{4}{5}+20i\)
Tập hợp các điểm biểu diễn số phức z thỏa mãn z ' = ( z + i ) ( z + i ) là một số thực và là đường thẳng có phương trình
A. x = 0
B. y = 0
C. x = y
D. x = -y
Gọi z1 z2 là các nghiệm phức của phương trình \(z^2+4z+7=0\) . Số phức \(z_1.\overline{z_2}+\overline{z_2}.z_1\) bằng
A:2
B:10
C:2i
D:10i
Chắc bạn ghi nhầm đề \(z_1\overline{z_2}+\overline{z_1}z_2\) mới có lý chứ nhỉ?
Khi pt bậc 2 có 2 nghiệm phức \(z_1;z_2\) thì \(z_1=\overline{z_2}\)
Do đó \(z_1\overline{z_2}+\overline{z_1}z_2=z_1^2+z_2^2=\left(z_1+z_2\right)^2-2z_1z_2=\left(-4\right)^2-2.7=2\)
Phương trình z 2 - a z + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
A. a = 2, b = -2
B. a = 2, b = 2
C. a = -2, b = 2
D. a = -2, b = -2
Thay z = 1 + i vào phương trình đã cho ta có:
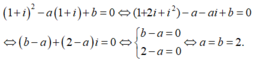
Chọn đáp án B.
Viết các phương trình bậc hai dạng x^2+px+q=0. Biết rằng, phương trình có 2 nghiệm nguyên , các hệ số p,q đều là những số nguyên và p+q+1=2003