Chọn C
Ta có: z 2 = - 1 + 2 2 i = 1 + 2 2 i + 2 i 2 = ( 1 + 2 i ) 2 <=> z 1 , 2 = ± ( 1 + 2 i )
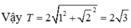
Chọn C
Ta có: z 2 = - 1 + 2 2 i = 1 + 2 2 i + 2 i 2 = ( 1 + 2 i ) 2 <=> z 1 , 2 = ± ( 1 + 2 i )
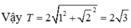
Cho phương trình \(z^2+bc+c=0\) có hai nghiệm z1 z2 thỏa mãn z2 - z1 = 4+2i . Gọi A,B là các điểm biểu diễn các nghiệm của phương trình \(z^2-2bz+4c=0\) . Tính độ dài đoạn AB
A: \(8\sqrt{5}\)
B: \(2\sqrt{5}\)
C: \(4\sqrt{5}\)
D: \(\sqrt{5}\)
Phương trình z 1 = 1 + 2 i , z 2 = 2 - 3 i có nghiệm là z = 2 + i khi
A. a = 1, b = 4
B. a = -1, b = 4
C. a = -1, b = -4
D. a = 1, b = -4
Gọi z1 z2 là hai nghiệm phức của phương trình \(z^2-4z+5=0\) . Tính:
w = \(\dfrac{1}{z_1}+\dfrac{1}{z_2}+i\left(z_1^2z_2+z^2_2z_1\right)\)
Phương trình \(z^2+az+b=0\) với a b là các số thực nhận số phức 1+i là một nghiệm.Tính a - b?
A:-2
B:-4
C:4
D:0
Gọi z1 z2 là các nghiệm phức của phương trình \(z^2+4z+7=0\) . Số phức \(z_1.\overline{z_2}+\overline{z_2}.z_1\) bằng
A:2
B:10
C:2i
D:10i
Phương trình z 2 - z + 1 = 0 có hai nghiệm là
A. 1 ± 3 i 2
B. - 1 ± 3 i 2
C. 1 ± 3 i
D. - 1 ± 3 i
Phương trình ( 1 + i ) 2 = - 7 + i có các nghiệm là
A. -1 - 2i và 1 + 2i
B. -1 + 2i và 1 + 2i
C. -1 + 2i và 1 - 2i
D. 1 + 2i và 1 - 2i
Gọi z1 , z2 là hai nghiệm phức của phương trình \(z^2-4z+5=0\) . Giá trị của biểu thức \(\left(z_1-1\right)^{2019}+\left(z_2-1\right)^{2019}\) bằng?
A: 21009
B: 21010
C:0
D: -21010
Tập hợp các điểm biểu diễn số phức z thỏa mãn z ' = ( z + i ) ( z + i ) là một số thực và là đường thẳng có phương trình
A. x = 0
B. y = 0
C. x = y
D. x = -y
Phương trình z 2 - a z + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
A. a = 2, b = -2
B. a = 2, b = 2
C. a = -2, b = 2
D. a = -2, b = -2