Giải các phương trình mũ: 1 5 x = 25

Những câu hỏi liên quan
Giải các phương trình sau (2x-5) mũ 3 - (3x-4) mũ 3 + (x+1) mũ 3=0
Đặt a = 2x - 5; b = 3x - 4 => x + 1 = b - a
Khi đó ta có pt: a3 - b3 + (b - a)3 = 0
<=> (b - a)3 - (b3 - a3) = 0
<=> b3 - a3 - b3 + a3 - 3ab(b - a)= 0
<=> 3ab(b - a) = 0 <=> a = 0 hoặc b = 0 hoặc a= b
* Với a = 0, ta có: 2x - 5 = 0 <=> x = \(\frac{5}{2}\)
* Với b = 0, ta có: 3x - 4 = 0 <=> x = \(\frac{4}{3}\)
* Với a = b, ta có: 2x - 5 = 3x - 4 <=> x = -1
Vậy S = {-1;\(\frac{4}{3}\);\(\frac{5}{2}\)}
Xem thêm câu trả lời
Giải các bất phương trình mũ sau: 1 3 x + 5 ≤ 1 3 x + 1 - 1
Đặt t = 3 x (t > 0) , ta có bất phương trình
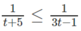
Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.
Từ đó ta có hệ:
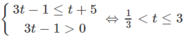
Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.
Đúng 0
Bình luận (0)
Giải các bất phương trình mũ sau:
4
x
-
2
x
+
1
+
8
2
1
-
x
8
x
Đọc tiếp
Giải các bất phương trình mũ sau: 4 x - 2 x + 1 + 8 2 1 - x < 8 x
2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0
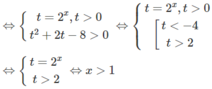
Đúng 0
Bình luận (0)
Giải các phương trình sau
(x-4) mũ 4 - (x-2) mũ 4=82
mình nhờ các bạn giải hộ vài bài với, mình xin cảm ơn rất nhiều
1. Giải phương trình
a) (x+5)(2x+1) - x2 + 25 = 0
b 3x/x-2 - x/x-5 + 3x/(x-2)(x-5) = 0
2 cho phương trình ẩn x
x+1/x+2+m = x+1/x+2-m
a) giải phương trình khi m = -3
b) tìm các giá trị m sao cho phương trình nhận x=3 làm nghiệm
1/a/\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=-6\end{cases}}}\)
Vậy ...................
b/ ĐKXĐ:\(x\ne2;x\ne5\)
.....\(\Rightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x^2-10x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\left(nhận\right)\\x=5\left(loại\right)\end{cases}}}\)
Vậy ..............
Đúng 0
Bình luận (0)
`Answer:`
`1.`
a. \(\left(x+5\right)\left(2x+1\right)-x^2+25=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x^2-25\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1-x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-6\\x=-5\end{cases}}}\)
b. \(\frac{3x}{x-2}-\frac{x}{x-5}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\left(ĐKXĐ:x\ne2;x\ne5\right)\)
\(\Leftrightarrow\frac{3x\left(x-5\right)}{\left(x-2\right)\left(x-5\right)}-\frac{x\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\frac{3x\left(x-5\right)-x\left(x-2\right)+3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow3x\left(x-5\right)-x\left(x-2\right)+3x=0\)
\(\Leftrightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\text{(Không thoả mãn)}\end{cases}}}\)
`2.`
\(ĐKXĐ:x\ne-m-2;x\ne m-2\)
Ta có: \(\frac{x+1}{x+2+m}=\frac{x+1}{x+2-m}\left(1\right)\)
a. Khi `m=-3` phương trình `(1)` sẽ trở thành: \(\frac{x+1}{x-1}=\frac{x+1}{x+5}\left(x\ne1;x\ne-5\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\\frac{1}{x-1}=\frac{1}{x+5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-1=x+5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\-1=5\text{(Vô nghiệm)}\end{cases}}}\)
b. Để phương trình `(1)` nhận `x=3` làm nghiệm thì
\(\Leftrightarrow\hept{\begin{cases}\frac{3+1}{3+2-m}=\frac{3+1}{3+2-m}\\3\ne-m-2\\3\ne m-2\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{4}{5+m}=\frac{4}{5-m}\\m\ne\pm5\end{cases}}\Leftrightarrow\hept{\begin{cases}5+m=5-m\\m\ne\pm5\end{cases}}\Leftrightarrow m=0\)
Bài 1. Giải các phương trình sau:
a) |4x2 - 25| = 0
b) |x - 2| = 3
c) |x - 3| = 2x - 1
d) |x - 5| = |3x - 2|
Lời giải:
a) $|4x^2-25|=0$
$\Leftrightarrow 4x^2-25=0$
$\Leftrightarrow (2x-5)(2x+5)=0$
$\Rightarrow x=\pm \frac{5}{2}$
b)
$|x-2|=3$
\(\Rightarrow \left[\begin{matrix} x-2=-3\\ x-2=3\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-1\\ x=5\end{matrix}\right.\)
c)
\(|x-3|=2x-1\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ \left[\begin{matrix} x-3=2x-1\\ x-3=1-2x\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\end{matrix}\right.\Rightarrow x=\frac{4}{3}\)
d)
$|x-5|=|3x-2|$
\(\Rightarrow \left[\begin{matrix} x-5=3x-2\\ x-5=2-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải các phương trình sau:
a) \({5^{2x - 1}} = 25\);
b) \({3^{x + 1}} = {9^{2x + 1}}\);
c) \({10^{1 - 2x}} = 100000\).
\(a,5^{2x-1}=25\\ \Leftrightarrow5^{2x-1}=5^2\\ \Leftrightarrow2x-1=2\\ \Leftrightarrow2x=3\\ \Leftrightarrow x=\dfrac{3}{2}\)
\(b,3^{x+1}=9^{2x+1}\\ \Leftrightarrow3^{x+1}=3^{4x+2}\\ \Leftrightarrow x+1=4x+2\\ \Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\)
\(c,10^{1-2x}=100000\\ \Leftrightarrow10^{1-2x}=10^5\\ \Leftrightarrow1-2x=5\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=-2\)
Đúng 0
Bình luận (0)
giải các phương trình sau về dạng phương trình tích
x^2+10x+25-4x(x+5)=0
\(x^2+10x+25-4x\left(x+4\right)\)
\(=x^2+10x+25-4x^2-16x\)
\(=-3x^2-6x+25\)
\(=-3.\left(x^2+2x-\frac{25}{3}\right)\)
đó dạng tích đó
Đúng 0
Bình luận (0)
giải các phương trình sau bằng cách đưa về phương trình tích
a) x^2+10x+25-4x(x+5)=0
b) (4x-5)^2-2(16x^2-25)=0
Tham khảo bài này :
(3x+1)(7x+3)=(5x-7)(3x+1)
<=> (3x+1)(7x+3)-(5x-7)(3x+1)=0
<=> (3x+1)(7x+3-5x+7)=0
<=> (3x+1)(2x+10)=0
<=> 2(3x+1)(x+5)=0
=> 3x+1=0 hoặc x+5=0
=> x= -1/3 hoặc x=-5
Vậy x = -1/3 hoặc x = -5
Đúng 0
Bình luận (0)
\(a,x^2+10x+25-4x\left(x+5\right)=0.\)
\(\Leftrightarrow\left(x+5\right)^2-4x\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(5-3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\5-3x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{5}{3}\end{cases}}}\)
\(b,\left(4x-5\right)^2-2\left(16x^2-25\right)=0\)
\(\Leftrightarrow\left(4x-5\right)^2-2\left(4x+5\right)\left(4x-5\right)=0\)
\(\Leftrightarrow-\left(4x-5\right)\left(4x+15\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x-5=0\\4x+15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=-\frac{15}{4}\end{cases}}}\)
Đúng 0
Bình luận (0)


















