Tìm các đường tiệm cận của đồ thị các hàm số sau: y = 2 x 2 + 8 x - 9 3 x 2 + x - 4

Những câu hỏi liên quan
Tìm các đường tiệm cận của đồ thị các hàm số sau: y = 5 x + 3 - x + 2
Tiệm cận đứng: x = 2; Tiệm cận ngang: y = -5
Đúng 0
Bình luận (0)
Xét các mệnh đề sau(1). Đồ thị hàm số
y
1
2
x
-
3
có hai đường tiệm cận đứng và một đường tiệm cận ngang(2). Đồ thị hàm số
y
x
+
x
2
+
x
+
1...
Đọc tiếp
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Đúng 0
Bình luận (0)
Cho các mệnh đề sau(1) Đường thẳng
y
y
0
là đường tiệm cận ngang của đồ thị hàm số y f(x) nếu
lim
x
→
x
0
f
x
y
0
h
o
ặ
c
lim
x...
Đọc tiếp
Cho các mệnh đề sau
(1) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → x 0 f x = y 0 h o ặ c lim x → x 0 f x = y 0
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu lim x → - ∞ f x = y 0 h o ặ c lim x → + ∞ f x = y 0
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = + ∞ h o ặ c lim x → x 0 - f x = - ∞
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu lim x → x 0 + f x = - ∞ h o ặ c lim x → x 0 - f x = - ∞
Trong các mệnh đề trên, số mệnh đề đúng là:
A. 1
B. 2
C. 3
D. 4
Chọn C
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
Đúng 0
Bình luận (0)
Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số: Áp dụng để tìm các tiệm cận của đồ thị hàm số y = 2 x + 3 2 - x
- Cách tìm tiệm cận ngang:
+ Tính các giới hạn 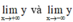
+ Nếu 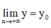 hoặc
hoặc 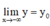 thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
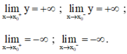
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định, liên tục trên tập R{1} và có bảng biến thiênSố mệnh đề đúng trong các mệnh đề sau là? 1. Đường thẳng y2 là đường tiệm cận ngang của đồ thị hàm số. 2. Đường thẳng x1 là đường tiệm cận đứng của đồ thị hàm số. 3. Hàm số đồng biến trên các khoảng
-
∞
;
1
và
1
;
+
∞
A. 0. B....
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
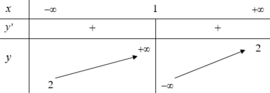
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3
Gọi số
n
∈
N
là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
. Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n ∈ N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 . Tìm n
A.1
B.0
C. 2
D. 3
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 Tìm n
A.1
B.0
C. 2
D. 3
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau: y = 2 x - 1 x + 2
Ta có:
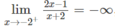
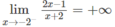
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
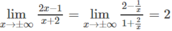
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
−
1
x
−
3
. Xét các mệnh đề sau:(1) Hàm số nghịch biến trên
D
ℝ
3
(2) Đồ thị hàm số có một tiệm cận đứng là x1, tiệm cận ngang là y3.(3) Hàm số đã cho không có cực trị(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng...
Đọc tiếp
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Đáp án B
Sai lầm thường gặp: Tập xác định D = ℝ \ 3 .
Đạo hàm y ' = − 2 x − 3 2 ,0, ∀ x ∈ D ⇒ Hàm số nghịch biến trên ℝ \ 3 , hoặc làm số nghịch biến trên − ∞ ; 3 ∪ 3 ; + ∞ . Hàm số không có cực trị.
Tiệm cận đứng: x=3; tiệm cận ngang: y=1. Đồ thị hàm số nhận giao điểm I 3 ; 1 của hai đường tiệm cận làm tâm đối xứng.
Từ đó nhiều học sinh kết luận các mệnh đề 1 , 3 , 4 đúng và chọn ngay A.
Tuy nhiên đây là phương án sai.
Phân tích sai lầm:
Mệnh đề (1) sai, sửa lại: hàm số nghịch biến trên mỗi khoảng − ∞ ; 3 và 3 ; + ∞ . Học sinh cần nhớ rằng, ta chỉ học định nghĩa hàm số đồng biến (nghịch biến) trên khoảng, đoạn, nửa khoảng; chứ không có trên những khoảng hợp nhau.
Mệnh đề (2) sai. Đồ thị hàm số có một tiệm cận đứng là x=3, một tiệm cận ngang là y=1.
Mệnh đề 3 , 4 đúng.
Đúng 0
Bình luận (0)



