Cho hypebol (H): 6 x 2 - 9 y 2 = 54. Phương trình một đường tiệm cận là:
A. y = 9 6 x
B. y = 6 9 x
C. y = 6 3 x
D. y = 3 6 x
Lập phương trình chính tắc của hypebol biết 1 tiêu điểm là F(-1; 0) và 1 đường tiệm cận là 3x + y = 0
Phương trình hai tiệm cận y = ± 2 3 x là của hypebol có phương trình chính tắc nào sau đây?
A. 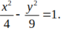
B. 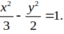
C.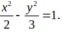
D. 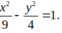
Chọn D.
Ta có: ± b a = ± 2 3 ⇒ a = 3 b = 2 .
Phương trình (H) : x 2 9 - y 2 4 = 1
Phương trình hai tiệm cận y = ± 2 3 x là của hypebol có phương trình chính tắc nào sau đây?
A. x 2 4 - y 2 9 = 1
B. x 2 3 - y 2 2 = 1
C. x 2 2 - y 2 3 = 1
D. x 2 9 - y 2 4 = 1
Đáp án: D
Hypebol có hai đường tiệm cận
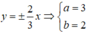
Vậy phương trình của hypebol là:
x 2 9 - y 2 4 = 1
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 - x - x + 2 có phương trình lần lượt là
A. x=1,y=2
B. x=2,y=1
C. x=2,y= 1 2
D. x=2,y=-1
Cho hàm số y = 3 − x x + 1 có đồ thị (H). Một phép dời hình biến (H) thành (H') có tiệm cận ngang y = 2 và tiệm cận đứng x = 2. Lấy đối xứng (H’) qua gốc toạ độ được hình (H''). Tìm phương trình của (H'')
A. y = 6 − 2 x x + 2
B. y = 2 x − 6 x + 2
C. y = − 2 x x + 2
D. y = 2 x x + 2
Đáp án C
Xét đồ thị hàm số y = 3 − x x + 1 đường tiệm cận ngang y = − 1 và đường tiệm cận đứng x = − 1 . Gọi I − 1 ; − 1 là giao điểm của hai đường tiệm cận của đồ thị (H). Gọi I ' 2 ; 2 là giao điểm của hai đường tiệm cận của đồ thị
Phép dời hình đồ thị (H )thành là phép tịnh tiến theo vecto v → = I I ' → = 3 ; 3
Giả sử đồ thị (H') có phương trình y = a x + b c x + d ; a d − b c ≠ 0
⇒ a c = 2 − d c = 2 ⇒ a = 2 c − d = 2 c ⇒ y = 2 c x + b 6 c − 2 c
Lấy
A 3 ; 0 ∈ H ⇒ A ' 6 ; 3 ∈ H ' ⇒ 12 c + b 6 c − 2 c = 3 ⇒ b = 0
Vậy H ' : y = 2 x x − 2 . Lấy đối xứng (H') qua gốc toạ độ ta được H ' ' : − y = − 2 x − x − 2 ⇒ y = − 2 x x + 2
Cho hàm số y = 3 − x x + 1 có đồ thị (H). Một phép dời hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2. Lấy đối xứng (H’) qua gốc toạ độ được hình (H”). Tìm phương trình của (H”)
A. y = 6 − 2 x x + 2
B. y = 2 x − 6 x + 2
C. y = − 2 x x + 2
D. y = 2 x x + 2
a) Cho hàm số 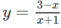 có đồ thị (H)
có đồ thị (H)
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’).
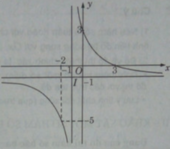
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
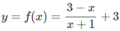
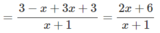
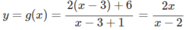
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là:
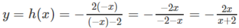
Cho hàm số y = x - 1 x - 2 . Đường tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình:
A. x = 1
B. x = 2
C. y = 1
D. y = 2
Chọn đáp án B
![]()
Do đó x = 2 là tiệm cận đứng của đồ thị hàm số.

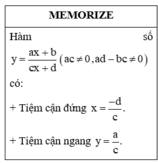
Phương trình đường tiệm cận ngang của đồ thị hàm số y = 2 + 3 1 − x là
A. x = 1
B. y = 2
C. y = 3
D. y = − 1
Đáp án B
Ta có
lim x → + ∞ y = 2 ⇒ T C N : y = 2 lim x → − ∞ y = 2 ⇒ T C N : y = 2