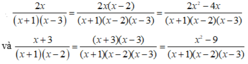Biến đổi 3 x ( x + 2 ) ( x − 1 ) và x + 3 ( x + 2 ) ( x − 3 ) với x ≠ − 2 ; x ≠ 1 và x ≠ 3 thành cặp phân thức bằng nó và có cùng mẫu thức.

Những câu hỏi liên quan
Bài 2: a) Tính \(\dfrac{3}{x-3}-\dfrac{6x}{9-x^2}+\dfrac{x}{x+3}\)
b) Biến đổi biểu thức hữu tỉ sau thành một phân tử \(2+\dfrac{2}{2+\dfrac{2}{x}}\)
Biến đổi vế trái thành vế phải :
x(x+1)(x+2)(x+3)+1 = (x2+3x+1)2
\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+x\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^3+x^2+2x^2+2x\right)\left(x+3\right)+1\)
\(=\left(x^3+3x^2+2x\right)\left(x+3\right)+1\)
\(=x^4+3x^3+2x^2+3x^3+9x^2+6x+1\)
\(=x^4+\left(3x^3+3x^3\right)+\left(2x^2+9x^2\right)+6x+1\)
\(=x^4+6x^3+11x^2+6x+1\)
\(=\left(x^2+3x+1\right)^2\) (Bằng vế phải)
Đúng 0
Bình luận (0)
\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left[x\left(x+3\right)\right]\left[\left(x+1\right)\left(x+2\right)\right]+1\)
\(=\left(x^2+3x\right)\left(x^2+2x+x+2\right)+1\)
\(=\left(x^2+3x+1-1\right)\left(x^2+3x+1+1\right)+1\)
\(=\left(x^2+3x+1\right)^2-1^2+1\)
\(=\left(x^2+3x+x\right)^2\)
Đúng 0
Bình luận (0)
Mk sửa lại dòng cuối nhé !
\(=\left(x^2+3x+1\right)^2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Hãy cho biết kết quả sau khi thực hiện thuật toán sau: Bước 1. Tam←x; Bước 2. x←y; Bước 3. y← tam; *
A.Khác
B.Giá trị của biến y bằng giá trị của biến x
C.Hoán đổi giá trị hai biến x và y
D.Giá trị của biến x bằng giá trị của biến y
Hãy cho biết kết quả sau khi thực hiện thuật toán sau:
Bước 1. Tam←x;
Bước 2. x←y;
Bước 3. y← tam;
A.
Khác
B.
Hoán đổi giá trị hai biến x và y
C.
Giá trị của biến y bằng giá trị của biến x
D.
Giá trị của biến x bằng giá trị của biến y
Dùng tính chất cơ bản của phân thức hoặc quy tắc đổi dấu để biến đổi mỗi cặp phân thức sau thành một cặp phân thức bằng nó và có cùng mẫu thức:
2
x
(
x
+
1
)
(
x
-
3
)
và
x
+
3
(
x
+...
Đọc tiếp
Dùng tính chất cơ bản của phân thức hoặc quy tắc đổi dấu để biến đổi mỗi cặp phân thức sau thành một cặp phân thức bằng nó và có cùng mẫu thức: 2 x ( x + 1 ) ( x - 3 ) và x + 3 ( x + 1 ) ( x - 2 )
Bài 4.a) Cho x + y 25 và x.y 136. Tính x2 + y2b) Cho x + y 3 và x2 + y2 5. Tính x3 + y3Gợi ý: Biến đổi x2 + y2 (x + y)2 – 2xy để tìm tích x.y Sau đó biến đổi x3 + y3 (x + y)3 – 3xy (x + y)c) Cho x – y 5 và x2 + y2 15. Tính x3 - y3
Đọc tiếp
Bài 4.
a) Cho x + y = 25 và x.y = 136. Tính x2 + y2
b) Cho x + y = 3 và x2 + y2 = 5. Tính x3 + y3
Gợi ý: Biến đổi x2 + y2 = (x + y)2 – 2xy để tìm tích x.y
Sau đó biến đổi x3 + y3 = (x + y)3 – 3xy (x + y)
c) Cho x – y = 5 và x2 + y2 = 15. Tính x3 - y3
a) Ta có x + y = 25
=> (x + y)2 = 625
=> x2 + y2 + 2xy = 625
=> x2 + y2 + 10 = 625
=> x2 +y2 = 615
b) Ta có x + y = 3
=> (x + y)3 = 27
=> x3 + 3x2y + 3xy2 + y3 = 27
=> x3 + y3 + 3xy(x + y) = 27
=> x3 + y3 + 9xy = 27
Lại có x + y = 3
=> (x + y)2 = 9
=> x2 + y2 + 2xy = 9
=> 2xy = 4
=> xy = 2
Khi đó x3 + y3 + 9xy + 27
=> x3 + y3 + 18 = 27
=> x3 + y3 = 9
c) Ta có x - y = 5
=> (x - y)2 = 25
=> x2 + y2 - 2xy = 25
=> 2xy = -10
=> xy = -5
Khi đó : x3 - y3 = (x - y)(x2 + xy + y2) = 5(15 - 5) = 5.10 = 50
Bài 4.
a) x2 + y2 = x2 + 2xy + y2 - 2xy
= ( x2 + 2xy + y2 ) - 2xy
= ( x + y )2 - 2xy
= 252 - 2.136
= 625 - 272
= 353
b) x + y = 3
⇔ ( x + y )2 = 9
⇔ x2 + 2xy + y2 = 9
⇔ 5 + 2xy = 9 ( gt x2 + y2 = 5 )
⇔ 2xy = 4
⇔ xy = 2
x3 + y3 = x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2
= ( x3 + 3x2y + 3xy2 + y3 ) - ( 3x2y + 3xy2 )
= ( x + y )3 - 3xy( x + y )
= 33 - 3.2.3
= 27 - 18
= 9
a) Ta có x + y = 25
=> (x + y)2 = 625
=> x2 + y2 + 2xy = 625
=> x2 + y2 + 2.136 = 625
=> x2 + y2 + 272 = 625
=> x2 + y2 = 353
Xem thêm câu trả lời
Câu 1:cho n thuộc N với n ko chia hết cho 3
CMR n^2 chia 3 dư 1
Câu 2:Cmr (a^4+b^4+a+b)^4=2*(a^2+ab+b^2)
Câu 3: Biến đổi (x^2+3x+1)^2-1 thành tích
Câu 4: Biến đổi (x^2-8)^2+36 thành tích
Biến đổi phân thức x^2-7/4x+3 với x khác -3/4 và x khác 0 thành 1 phần thức bằng nó và có mẫu thức B=12x^2+9x
biến đổi |x+1| - 2|x+1=2