Gọi các kích thước của hình hộp lần lượt là a, b, c (a, b, c > 0)

Theo đề bài ta có a² + b² + c²= d²

Diện tích toàn phần của hình hộp là:

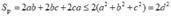
Dấu "=" xảy ra Û a = b = c.

Vậy hình hộp có diện tích toàn phần lớn nhất là hình lập phương.

do la hinh vuong co canh la 4

4*4=16 lon nhat trong cac hinh chu nhat co chu vi la 16

Nửa chu vi là :

16 : 2 = 8 = 1 + 7 = 2 + 6 = 3 + 5 = 4 + 4
Những hình chữ nhật cần tìm là những hình chữ nhật có ( chiều dài ; chiều rộng) =  (  7; 1 )  , ( 6 ; 2 ) , ( 5 ; 3 ) , ( 4 ; 4 )
Trong những hình chữ nhật tìm được :  Hình chữ nhật có chiều dài 4 cm ,chiều rộng 4 cm có diện tích lớn nhất  là 16 cm2
Lưu ý hình vuông là hình chữ nhật đặc biệt

cảm ơn

hình có diện tích lớn nhất là hình vuông nha bạn :)

Gọi x,y là kích thước của hình chữ nhật (x,y>0)

ta có: x²+y²=d²(đl pytago)

Từ (x-y)²>= 0 suy ra x²-2xy+y²>=0 suy ra x²+y²>= 2xy

Ta có xy<= d²/2, không đổi.

dấu ''='' xảy ra <=> x=y

suy ra ABCD là hình vuông

Vậy trong tất cả các hình chữ nhật có chiều dài đường chéo d không đổi thì hình vuông có diện tích lớn nhất và bằng d²/2

Gọi x,y là kích thước của hình chữ nhật (x,y>0)

ta có: x2+y2=d2(đl pytago)

Từ (x-y)2>= 0 suy ra x2-2xy+y2>=0 suy ra x2+y2>= 2xy

Ta có xy<= d2/2, không đổi.

dấu ''='' xảy ra <=> x=y

suy ra ABCD là hình vuông

Vậy trong tất cả các hình chữ nhật có chiều dài đường chéo d không đổi thì hình vuông có diện tích lớn nhất và bằng d2/2