Hàm số xác định trên f ( x ) = x - 1 x 3 . Đạo hàm của hàm f(x) là:
A. f ' x = 3 2 x - 1 x - 1 x x + 1 x 2 x
B. f ' x = 3 2 x + 1 x + 1 x x + 1 x 2 x
C. f ' x = 3 2 - x + 1 x + 1 x x + 1 x 2 x
D. f ' x = x x - 3 + 3 x - 1 x x
Những câu hỏi liên quan
Xét các khẳng định sau i) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn tại
α
∈
-
1
;
1
thỏa mãn
f
(
x
)
≥
f
(
α
)
∀
x
∈
-
1
;
1
. ii) Nếu hàm số y f(x) xác định trên [-1;1] thì tồn...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại α ∈ - 1 ; 1 thỏa mãn f ( x ) ≥ f ( α ) ∀ x ∈ - 1 ; 1 .
ii) Nếu hàm số y = f(x) xác định trên [-1;1] thì tồn tại β ∈ - 1 ; 1 thỏa mãn f ( x ) ≤ f ( β ) ∀ x ∈ - 1 ; 1 .
iii) Nếu hàm số y = f(x) xác định trên [-1;1] thỏa mãn f(-1).f(1)<0 thì tồn tại γ ∈ - 1 ; 1 thỏa mãn f ( γ ) = 0
Số khẳng định đúng là
A. 3.
B. 2.
C. 1.
D. 0.
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)
Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số yf(x) xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)f(x) +x . A. Không có giá trị B. x 0 C. x 1 D. x 2
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x) +x .
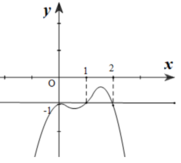
A. Không có giá trị
B. x = 0
C. x = 1
D. x = 2
Cho hàm số yf(x) xác định và liên tục trên R, có đạo hàm f(x). Biết rằng đồ thị hàm số f(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)f(x)+x. A. Không có giá trị
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R, có đạo hàm f'(x). Biết rằng đồ thị hàm số f'(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x)+x.
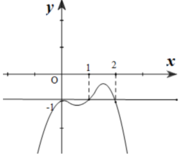
A. Không có giá trị
Hàm số y f(x) xác định, liên tục trên R và đạo hàm
f
(
x
)
2
(
x
-
1
)
2
(
2
x
+
6
)
. Khi đó hàm số f(x) A. Đạt cực đại tại điểm x 1 B. Đạt cực tiểu tại điểm x -3 C. Đạt cực đại tại điểm x -3 D. Đạt cực tiểu tại điểm x 1
Đọc tiếp
Hàm số y= f(x) xác định, liên tục trên R và đạo hàm f ' ( x ) = 2 ( x - 1 ) 2 ( 2 x + 6 ) . Khi đó hàm số f(x)
A. Đạt cực đại tại điểm x= 1
B. Đạt cực tiểu tại điểm x= -3
C. Đạt cực đại tại điểm x= -3
D. Đạt cực tiểu tại điểm x= 1
Cho hàm số y f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) (1–x)(x+2)g(x)+2018 với g(x) 0,
∀
x
∈
R
. Hàm số y f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào? A.
1
;
+
∞
B.
0
;...
Đọc tiếp
Cho hàm số y = f (x) xác định trên R và có đạo hàm f’(x) thỏa f’(x) = (1–x)(x+2)g(x)+2018 với g(x) < 0, ∀ x ∈ R . Hàm số y = f(1 – x) + 2018x + 2019 nghịch biến trên khoảng nào?
A. 1 ; + ∞
B. 0 ; 3
C. - ∞ ; 3
D. 3 ; + ∞
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra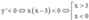 
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .
Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)
Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.
Đúng 0
Bình luận (0)
Xác định một hàm số y f(x) thoả mãn đồng thời các điều kiện sauf(x) xác định trên R {1}
lim
x
→
1
f
(
x
)
+
∞
;
lim
x
→
+
∞
f...
Đọc tiếp
Xác định một hàm số y = f(x) thoả mãn đồng thời các điều kiện sau
f(x) xác định trên R\ {1}
lim x → 1 f ( x ) = + ∞ ; lim x → + ∞ f ( x ) = 2 ; lim x → - ∞ f ( x ) = 2
Chẳng hạn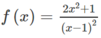 
.
Dễ dàng kiểm tra được rằng f(x) thoả mãn các điều kiện đã nêu
Đúng 0
Bình luận (0)
Cho hàm số \(y = f(x)\) xác định trên \(R\) có đạo hàm \(f'(x)=-(x+2)(x-1)^2(x-3)\)
Số điểm cực tiểu của hàm số \(f(x^2-2x)\) là?
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
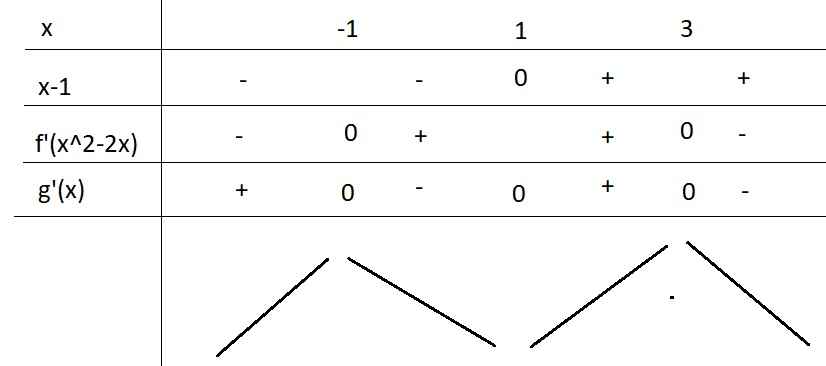
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu
Đúng 1
Bình luận (0)
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x)
x
(
x
2
-
1
)
(
x
-
4
)
,
∀
x
∈
R
. Hàm số
g
(
x
)
(
f
(
x
)
)
2
-
2
f...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp 3 xác định và liên tục trên R thoả mãn f(x)f‴(x) = x ( x 2 - 1 ) ( x - 4 ) , ∀ x ∈ R . Hàm số g ( x ) = ( f ' ( x ) ) 2 - 2 f ( x ) f '' ( x ) đồng biến trên khoảng nào ?
A. (0;1).
B. (-1;0).
C. ( 4 ; + ∞ ) .
D. ( - ∞ ; - 1 ) .
