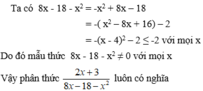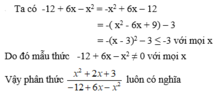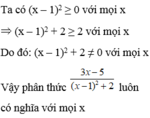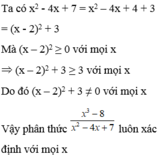Chứng minh các phân thức sau luôn xác định 2 x - 1 2 x 2 + 2 x + 1

Những câu hỏi liên quan
Chứng minh các phân thức sau luôn xác định với mọi x
2 x + 3 8 x - 18 - x 2
Chứng minh các phân thức sau luôn xác định với mọi x
x 2 + 2 x + 3 - 12 + 6 x - x 2
Chứng minh các phân thức sau luôn có nghĩa 3 x - 5 ( x - 1 ) 2 + 2
Chứng minh các phân thức sau luôn có nghĩa 5 ( x - 1 ) 2 + 1
Cho phân thức \(\frac{3x^3+6x^2}{x^3+x^2+x+2}\)
a) Tìm điều kiện của x để giá trị của phân thức được xác định
b) Chứng tỏ rằng giá trị của phân thức luôn luôn không âm khi nó được xác định
cho biểu thức
P=\(\dfrac{2}{x^4-1}-\dfrac{1}{1-x^2}\)
a,tìm điều kiện xác định của biểu thức P
b, chứng minh giá trị P luôn âm với x≠+-1
a) ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
b) Ta có: \(P=\dfrac{2}{x^4-1}-\dfrac{1}{1-x^2}\)
\(=\dfrac{2}{\left(x^2-1\right)\left(x^2+1\right)}+\dfrac{1}{x^2-1}\)
\(=\dfrac{2+x^2-1}{\left(x^2-1\right)\left(x^2+1\right)}\)
\(=\dfrac{x^2+1}{\left(x^2-1\right)\left(x^2+1\right)}\)
\(=\dfrac{1}{x^2-1}\)
Đúng 0
Bình luận (0)
Chứng minh các phân thức sau luôn xác định x 3 - 8 x 2 - 4 s + 7
Cho phân thức:\(\frac{3x^2+6x^2}{x^3+2x^2+x+2}\)
a) Tìm điều kiện của x để giá trị của phân thức được xác định ?
b) Chứng tỏ rằng giá trị của phân thức luôn không âm khi nó được xác định
\(\frac{3x^2+6x^2\left(xemlai\right)6x^2hay\left(6x\right)}{x^3+2x^2+x+2}=\frac{9x^2\left(culamtheode\right)}{x^3\left(x+2\right)+x+2=9}=\frac{9x^2}{\left(x^3+1\right)\left(x+2\right)}=\frac{9x^2}{\left(x+1\right)\left(x+2\right)\left(x^2-x+1\right)}\)
a)
\(x+1\ne0;x+2\ne0;x^2-x+1\ne0\)
\(x\ne-1;-2\)
b) khi 1<x<2 gia tri phan thuc <0 (-) xem lai
Đúng 0
Bình luận (0)
1/ Chứng minh đa thức sau luôn dương với mọi x:
x2 - x + 1
2/ Chứng minh các đa thức sau luôn âm với mọi x:
a) (x - 3)(1 - x) - 2
b) (x + 4)(2 - x) - 10
\(1,x^2-x+1=x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0=>\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\) (với mọi x)
Vậy ........
\(2,a,\left(x-3\right)\left(1-x\right)-2=x-x^2-3+3x-2=-x^2+4x-5=-\left(x^2-4x+5\right)\)
\(=-\left(x^2-4x+4+1\right)=-\left(x^2-2.x.2+2^2+1\right)=-\left[\left(x-2\right)^2+1\right]=-1-\left(x-2\right)^2\)
Vì \(\left(x-2\right)^2\ge0=>-\left(x-2\right)^2\le0=>-1-\left(x-2\right)^2\le-1< 0\) (với mọi x)
Vậy........
\(b,\left(x+4\right)\left(2-x\right)-10=2x-x^2+8-4x-10=-x^2-2x-2=-\left(x^2+2x+2\right)=-\left(x^2+2x+1+1\right)\)
\(=-\left(x^2+2.x.1+1^2+1\right)=-\left(x+1\right)^2+1=-1-\left(x+1\right)^2\le-1< 0\) (với mọi x)
Vậy.......
Đúng 0
Bình luận (0)