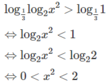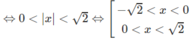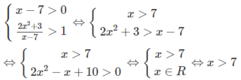Giải các bất phương trình logarit sau: 1 5 - logx + 2 1 + log x < 1

Những câu hỏi liên quan
Giải các phương trình logarit sau: log x + log x 2 = log 9 x
Với điều kiện x > 0, ta có
log x + 2 log x = log9 + log x
⇔ logx = log3 ⇔ x = 3
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau: log 3 x - 3 + log 3 x - 5 < 1
Giải các bất phương trình logarit sau: log 1 3 x - 1 ≥ - 2
Giải các bất phương trình sau: (x − 5)(logx + 1) < 0
Giải các bất phương trình logarit sau: 4 log 4 x - 33 log x 4 ≤ 1
Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: ![]()
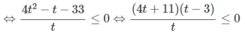
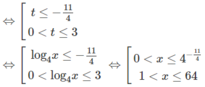
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:a) (2x − 7)ln(x + 1) 0;b) (x − 5)(logx + 1) 0;c) 2
log
3
2
x
+ 5
log
2
2
x
+
log
2
x
– 2 ≥ 0d) ln(3
e
x
− 2) ≤ 2x
Đọc tiếp
Giải các bất phương trình sau:
a) (2x − 7)ln(x + 1) > 0;
b) (x − 5)(logx + 1) < 0;
c) 2 log 3 2 x + 5 log 2 2 x + log 2 x – 2 ≥ 0
d) ln(3 e x − 2) ≤ 2x
a) Bất phương trình đã cho tương đương với hệ sau:
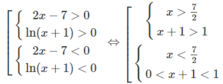
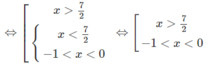
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )
b) Tương tự câu a), tập nghiệm là (1/10; 5)
c) Đặt t = log 2 x , ta có bất phương trình 2 t 3 + 5 t 2 + t – 2 ≥ 0 hay (t + 2)(2 t 2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2
Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2
Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )
d) Bất phương trình đã cho tương đương với hệ:
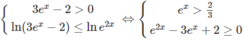
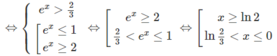
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau:
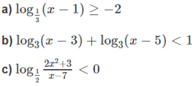
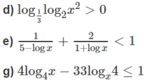
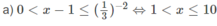
b)
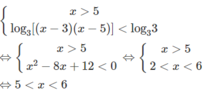
c)
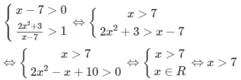
d)
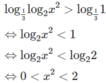
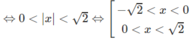
e) Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
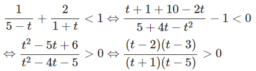
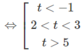
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < 1/10 hoặc 100 < x < 1000 hoặc x > 100 000.
g) Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: 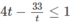
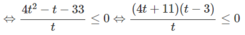
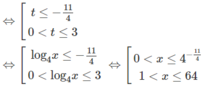
Đúng 0
Bình luận (0)
Giải các bất phương trình logarit sau: log 1 3 log 2 x 2 > 0
Giải các bất phương trình logarit sau: log 1 2 2 x 2 + 3 x - 7 < 0