Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: ![]()
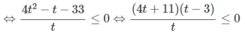
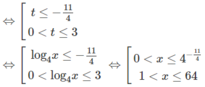
Với điều kiện x > 0, x ≠ 1 đặt t = log 4 x
ta có: ![]()
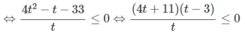
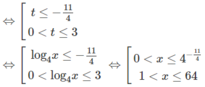
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Tập nghiệm của bất phương trình
log ( x 2 - 4 ) > log ( 3 x ) là:
![]()
![]()
![]()
![]()
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()
Giải bất phương trình log x + log ( x + 9 ) > 11
A. x > 1
B. x < 0 hoặc x > 3
C. x < 1 hoặc x > 2
D. 0 < x < 1 hoặc 2 < x < 3
Giải phương trình logx = log(x + 3) - log(x - 1)
A. x = 1
B. x = 3
C. x = 4
D. x = -1, x = 3
Giải các phương trình sau: (5 − x).log(x − 3) = 0
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Giải các phương trình sau:
a) e 2 + ln x = x + 3;
b) e 4 - ln x = x;
c) (5 − x).log(x − 3) = 0
Giải bất phương trình l o g ( x 2 - 2 x - 2 ) ≤ 0
A. [-1; 3]
B. ( 1 - 3 ; 1 + 3 )
C. [ - 1 ; 1 - 3 ) ∪ ( 1 + 3 ; 3 ]
D. (-∞; -1) ∪ (3; +∞)
Giải bất phương trình l o g ( x 2 - 2 x - 2 ) ≤ 0
A. [-1; 3]
B. ( 1 - 3 ; 1 + 3 )
C. [ - 1 ; 1 - 3 ) ∪ ( 1 + 3 ; 3 ]
D. (-∞; -1) ∪ (3; +∞)