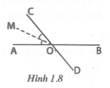
Vẽ hai đường thẳng MN và uv cắt nhau tại O. Trên tia Ou lấy điểm F, trên tia Ov lấy điểm E sao cho O là trung điểm  của EF. Điểm K trên tia Om sao cho OK= OE. Lấy điểm I trên tia On, vẽ tia FI. Đoạn thẳng FK, đường thẳng KE. Qua O kẻ đường xy sao cho xy ko cắt đoạn thẳng FK.

a. Kể tên hai tia đối nhau gốc E.

b. Kể tên hai tia trùng nhau gốc I.

Các bạn vẽ hình cho mik nhé, mik đang cần gấp.

Cho tam giác ABC nội tiếp đường tròn (O). Tia phân giác trong của góc A cắt đường tròn (O) tại điểm M.

a) Đường phân giác ngoài của góc A cắt lại đường tròn (O) tại N. CM M, O, N thẳng hàng.

b) Giả sử đường phân giác góc ngoài cắt đường thẳng BC tại E . CM góc AMO = góc CEA

c) Trên cạnh AC lấy điểm D tùy ý ( khác A và C). Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai F. Đường thẳng qua A  vuông góc với AB và đường thẳng qua F vuông góc với FC cắt nhau tại P. Chứng tỏ rằng P, D, O thẳng hàng.

1.Cho tam giác ABC có AD là tia phân giác trong của góc A. Quá D kẻ đường thẳng song song với AB cắt AC ở E và đường thẳng song song với AC cắt AB ở F.

a) Tứ giác AEDF là hình gì? Vì Sao?

b) Đường tròn đường kính AD cắt AB và AC lần lượt tại các điểm M và N. Chứng minh rằng: MN//EF.

2. Cho hai đường tròn (O;R) và(O';R') tiếp xúc trong với nhau tại A, (R>R'). Qua điểm B bất kỳ trên(O') vẽ tiếp tuyến với (O') cắt (O) tại hại điểm M và N, AB cắt (O) tại C. Chứng minh rằng:

a) MN vuông góc với OC

b) AC là tia phân giác của góc MAN

Bài 4 : ( 3,5 điểm) Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O; R) (với AB < AC). BE và CF là 2 đường cao của tam giác cắt nhau tại H

a) Chứng minh tứ giác BEFC và AEHF là tứ giác nội tiếp

b) Đường thẳng EF cắt đường thẳng BC tại S và EF cắt đường tròn (O) tại M và N (M nằm giữa S và E). Chứng minh SM. SN = SE. SF

c) Tia CE cắt đường tròn (O) tại K, vẽ dây KI song song với EF.

Chứng minh H, K đối xứng nhau qua AB

d) Chứng minh 3 điểm H, F, I thẳng hàng.