Tập nghiệm của bất phương trình x - 1 x - 3 > 1
A. S = 3 ; + ∞
B. S = ℝ
C. S = ∅
D. S = - ∞ ; 5
1/ Với giá trị nào của x thì 2 bất phương trình sau đây tương đương: (a-1)x - a+3>0 và ( a+1)x-a+2>0
2/ Bất phương trình: 5x/5 - 13/21 + x/15 < 9/25- 2x/35 có nghiệm là....
3/ Bất phương trình: 5x-1 < 2x/5 + 3 có nghiệm là...
4/ Bất phương trình: (x+4/x^2-9) -(2/x+3) < (4x/3x-x^2) có nghiệm nguyên lớn nhất là...
5/ Các nghiệm tự nhiên bé hơn 4 của bất phương trình (2x/5) -23 < 2x -16
6/ Các nghiệm tự nhiên bé hơn 6 của bất phương trình: 5x - 1/3 > 12 - 2x/3
7/ Bất phương trình: 2(x-1) - x > 3(x-1) - 2x-5 có tập nghiệm là...
8/ Bất phương trình: (3x+5/2) -1< (x+2/3)+x có tập nghiệm là...
9/ Bất phương trình: /x+2/ - /x-1/ < x - 3/2 có tập nghiệm là
10/ Bất phương trình: /x+1/ + /x-4/ > 7 có nghiệm nguyên dương nhỏ nhất là....
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Mình không biết sin lỗi vạn
Gọi S1 là tập nghiệm của bất phương trình log 2 ( x + 5 ) + log 1 2 ( 3 - x ) ≥ 0 và S2 là tập nghiệm của bất phương trình log2(x + 1) ≥ 1. Khẳng định nào dưới đây đúng ?
A. S 1 ∩ S 2 = [ 1 ; 3 )
B. S 1 ∩ S 2 = [ - 1 ; 3 )
C. S 1 ∩ S 2 = - 1 ; 1
D. S 1 ∩ S 2 = 1 ; 3
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
Tập nghiệm của bất phương trình 2 x + 2 ( x + 1 ) ≤ 3 x + 3 ( x - 1 )
A. x ∈ [ 2 ; + ∞ )
B. x ∈ 2 ; + ∞
C. x ∈ - ∞ ; 2
D. 2 ; + ∞
tập nghiệm của bất phương trình (x-1)(x+3)\(\ge\)0
Ta có: \(x-1=0\Rightarrow x=1\),\(x+3=0 \Rightarrow x = - 3\)
BXD:
Vậy \(T=(-\infty;-3]\cup[1;+\infty)\)
- Đặt \(f\left(x\right)=\left(x-1\right)\left(x+3\right)\)
- Cho \(f\left(x\right)=0\Rightarrow\left\{{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
- Lập bảng xét dấu :
x___________-3_________________1______________
x-1____-_____|________-_________0______+___________
x+3___-______0_______+_________|_____+____________
f(x)___+______0_______-__________0_____+____________
- Từ bảng xét dấu :- Để f(x) \(\ge0\)
Vậy phương trình có tập nghiệm \((-\infty;-3]\cup[1;+\infty)\)
Bài 3 :Cho bất phương trình : 3x(2x + 5) x(6x -1) + 4
a) Giải bất phương trình và biểu diễn tập nghiệm trên trục số.
b) Tìm nghiệm nguyên nhỏnhất của bất phương trình trên.
Tìm tập nghiệm của bất phương trình:
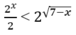
A. x < 3 B. x ≥ 1
C. 1 ≤ x < 3 D. x < 1
Cho bất phương trình: (x+2m)(x+1)>0. Tìm m để tập nghiệm của bất phương trình chứa (1;+∞)
- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)
Với m là tham số thực dương khác 1. Hãy tìm tập nghiêm S của bất phương trình log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x . Biết rằng x = 1 là một nghiệm của bất phương trình
A. S = − 2 ; 0 ∪ 1 3 ; 3
B. S = − 1 ; 0 ∪ 1 3 ; 2
C. S = − 1 ; 0 ∪ 1 3 ; 3
D. S = − 1 ; 0 ∪ 1 ; 3
Đáp án C
Vì x = 1 là một nghiệm của bất phương trình
⇒ log m 4 ≤ log m 2 ⇔ log m 2 ≤ 0 ⇔ m ∈ 0 ; 1 .
Khi đó, bất phương trình
log m 2 x 2 + x + 3 ≤ log m 3 x 2 − x ⇔ 3 x 2 − x > 0 2 x 2 + x + 3 ≥ 3 x 2 − x ⇔ − 1 ≤ x < 0 1 3 < x ≤ 3 .