Cho hai elíp E 1 : x 2 9 + y 2 4 = 1 v à E 2 : x 2 16 + y 2 1 = 1 Gọi E 1 ∩ E 2 = A , B , C , D Lập phương trình đường tròn ngoại tiếp hình chữ nhật ABCD.
A.11x2+ 11y2= 92
B. x2+ y2= 1
C. x2+ y2= 11
D. tất cả sai
Cho elíp E : x 2 16 + y 2 9 = 1 và đường thẳng d: 3x+ 4y -12= 0. Số giao điểm của đường thẳng d và elip (E) là:
A. 0
B.1
C. 2
D. 3
Ta có d: 3x+ 4y -12= 0 ⇔ y = 3 - 3 x 4 , thay vào phương trình E : x 2 16 + y 2 9 = 1 ta được
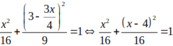
=> 2 x 2 - 8 x = 0
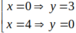
Vậy d luôn cắt (E) tại hai điểm phân biệt A(0;3) và B(4;0).
Chọn C
Cho elíp E : x 2 25 + y 2 9 = 1 và đường thẳng d: x- 2y +12= 0. điểm M trên (E) sao cho khoảng cách từ điểm M đến đường thẳng d là lớn nhất, nhỏ nhất.Tìm GTLN; GTNN đó?
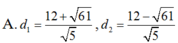
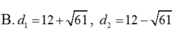
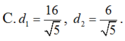
D. Đáp án khác
Đáp án A
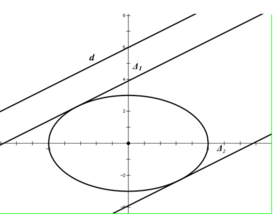
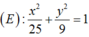 có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
có độ dài nửa trục lớn a = 5và độ dài nửa trục bé b= 3
Gọi ![]() là tiếp tuyến của (E) mà
là tiếp tuyến của (E) mà ![]() song song với d
song song với d
=> x- 2y + C = 0.
Vì d tiếp xúc với (E) nên ta có:
![]()
Nên ta có hai tiếp tuyến của (E) song song với d là:
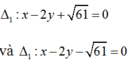
Vậy khoảng cách từ M đến đường thẳng d là lớn nhất là:
 , khoảng cách từ M đến đường thẳng d là bé nhất là:
, khoảng cách từ M đến đường thẳng d là bé nhất là:
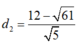
Trong mặt phẳng với hệ tọa độ Oxy, cho elíp : E : x 2 4 + y 2 = 1 và điểm C( 2;0) .Tìm tọa độ các điểm A; B trên (E), biết rằng hai điểm đối xứng nhau qua trục hoành và tam giác ABC là tam giác đều và điểm A có tung độ dương .
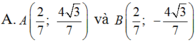
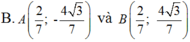
![]()
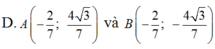
Đáp án A
Giả sử A( x0 ; y0) , Do A ; B đối xứng nhau qua Ox nên B( x0 ; -y0).
Ta có:
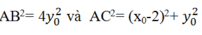
Vì A thuộc (E) nên:
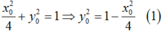
Vì AB = AC nên:
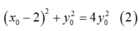
Thay (1) vào (2) ta được:
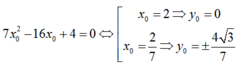
Vì điểm A khác C và Acó tung độ dương nên:
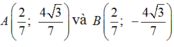
Cho Elip (E): \(\frac{x^2}{25}+\frac{y^2}{9}=1\) và đường thẳng (d): x= - 4 cắt (E) tại hai điểm M,N. Khi đó: a. MN=9/5 b. MN=9/25 c. MN=18/5 d. MN=18/25
Thay \(x=-4\) vào pt elip ta được:
\(\frac{y^2}{9}=1-\frac{16}{25}=\frac{9}{25}\Rightarrow\left[{}\begin{matrix}y=\frac{9}{5}\\y=-\frac{9}{5}\end{matrix}\right.\)
\(\Rightarrow MN=2.\frac{9}{5}=\frac{18}{5}\)
tìm x và y :
a. y x 2/3 = 1/4 + 1 b. y + 2/9 x 2 = 1 c. 4/9 : x = 2/7 : 3
d. 15/14 - y x 2 = 3/7 e. y : 5/16 = 1/3 + 5/6
khoanh câu trl đúng :
Hai đường chéo của hình thoi có độ dài lần lượt là 12 dm và 8 dm . Diện tích của hình thoi là : a.96 dm2 b.48 dm2 c.192 dm2 d.128 dm2
Một hình thoi có độ dài hai đường chéo lần lượt là 20 cm và 15 cm . Diện tích của hình thoi đó là : a.150 cm2 b.120 cm2 c.70 cm2 d.35 cm2
\(y\times\dfrac{2}{3}=\dfrac{1}{4}+\dfrac{1}{1}\)
\(y\times\dfrac{2}{3}=\dfrac{1}{4}+\dfrac{4}{4}\)
\(y\times\dfrac{2}{3}=\dfrac{5}{4}\)
\(y=\dfrac{5}{4}:\dfrac{2}{3}\)
\(y=\dfrac{5}{4}\times\dfrac{3}{2}\)
\(y=\dfrac{15}{8}\)
Bài 1: Cho hai số thực x,y (x>y) thỏa mãn x+y =5 và xy=3. Tính x^2+y^2, x^3+y^3 và x-y
giúp e với ạ, e cảm ơn
x^2+y^2=(x+y)^2-2xy
=5^2-2*3
=25-6
=19
x^3+y^3=(x+y)^3-3xy(x+y)
=5^3-3*3*5
=125-9*5
=80
(x-y)^2=(x+y)^2-4xy=5^2-4*3=13
=>\(x-y=\sqrt{13}\)
cho x;y là hai số dương thỏa mãn x^2+y^2=4 .tìm gt nhỏ nhất của e=(x+1/y)^2+(y+1/x)^2
Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho elip $\left( E \right)$ có phương trình: $\dfrac{{ x^2}}{9}+\dfrac{{{y}^2}}{4}=1$. Gọi ${{F}_{1}}, \, {{F}_2}$ là hai tiêu điểm của $\left( E \right)$. Tìm điểm $M$thuộc $\left( E \right)$ sao cho góc $\widehat{{{F}_{1}}M{{F}_2}}$ bằng ${{90}^{\circ}}$.
Gọi M(x,y)
Trong (E) có : \(c=\sqrt{a^2-b^2}=\sqrt{5}\)
Từ đó ta có : \(F_1\left(\sqrt{5};0\right);F_2\left(-\sqrt{5};0\right)\); \(F_1F_2=2\sqrt{5}\)
=> \(\overrightarrow{F_1M}\left(x-\sqrt{5};y\right)\Rightarrow F_1M^2=\left(x-\sqrt{5}\right)^2+y^2\)
tương tự \(F_2M^2=\left(x+\sqrt{5}\right)^2+y^2\)
Do \(\widehat{F_1MF_2}=90^{\text{o}}\) nên tam giác F1MF2 vuông tại M
=> F1M2 + F2M2 = F1F22
<=> \(\left(x-\sqrt{5}\right)^2+y^2+\left(x+\sqrt{5}\right)^2+y^2=20\)
\(\Leftrightarrow x^2+y^2=5\)
Lại có \(M\in\left(E\right)\Rightarrow\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
từ đó ta có hệ \(\left\{{}\begin{matrix}x^2+y^2=5\\\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=\dfrac{9}{5}\\y^2=\dfrac{16}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\pm\dfrac{3\sqrt{5}}{5}\\y=\pm\dfrac{4\sqrt{5}}{5}\end{matrix}\right.\)
Cho Elip (E): \(\dfrac{x^2}{9}+\dfrac{y^2}{a}=1\). Tìm (E') là ảnh của (E) qua phép tịnh tiến theo v(2;1)