Cho bảng tần số, tần suất ghép lớp như câu 22. Hãy điền số thích hợp vào**
A. 10
B. 12
C. 8
D. 13
Cho bảng tần số, tần suất ghép lớp như câu 22. Hãy điền số thích hợp vào***
A. 3,9%
B. 5,9%
C. 13,9%
D. 23,9%
Áp dụng công thức tính tần suất ta có tần suất của lớp thứ 4 là:
5 36 . 100 % = 13,9 %
Chọn C.
Cho bảng tần số, tần suất ghép lớp như sau
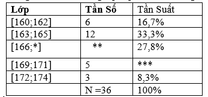
Hãy điền số thích hợp vào*
A. 167
B. 168
C. 169
D. 164
Độ dài mỗi lớp là: 162-160= 2.
Do đó số cần tìm là: 166+ 2= 168
Chọn B
Cho bảng tần số, tần suất ghép lớp như sau:
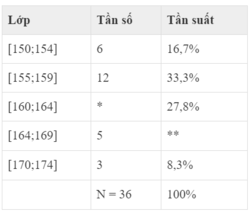
a) Giá trị * là:
A. 8 B. 10
C. 12 D. 13
b) Giá trị ** là:
A. 3,9% B. 5,9%
C. 13,9% D. 23,9%
Dựa vào bảng phân bố tần số, tần suất ghép lớp ta có:
a) Giá trị của * là:
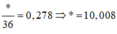
Đáp án: B
b) Giá trị của ** là:

Đáp án C
Cho bảng phân bố tần số và tần suất ghép lớp sau:
Nhiệt độ trung bình của tháng 12 tại thành phố Vinh từ 1961 đến hết 1990 (30 năm)
| Lớp nhiệt độ (oC) | Tần số | Tần suất (%) |
| [12; 14) | 1 | 3,33 |
| [14; 16) | 3 | 10,00 |
| [16; 18) | 12 | 40,00 |
| [18; 20) | 9 | 30,00 |
| [20; 22] | 5 | 16,67 |
| Cộng | 30 | 100 % |
a) Hãy tính số trung bình cộng của bảng 6 và bảng 8.
b) Từ kết quả đã tính được ở câu a), có nhận xét gì về nhiệt độ ở thành phố Vinh trong tháng 2 và tháng 12 (của 30 năm được khảo sát)
a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
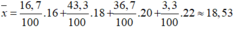
Số trung bình cộng của bảng 8 là:
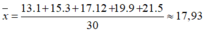
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.
Cho các số liệu thống kê được ghi trong hai bảng sau
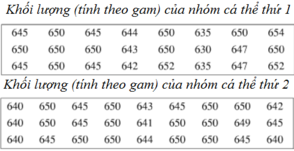
a) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là
[630; 635) ; [635;640) ; [640; 645) ; [645; 650) ; [650; 655)
b) Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là:
[638;642) ; [642; 646) ; [646;650) ; [650; 654] ;
c) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất
d) Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu b) bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e) Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố đã lập được
Từ đó, xét xem nhóm cá nào có khối lượng đồng đều hơn
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
c) Biểu đồ tần suất hình cột:
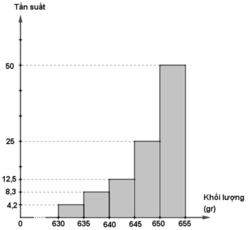
- Đường gấp khúc tần suất
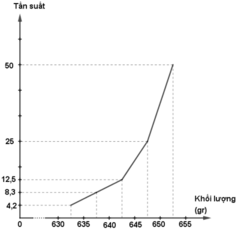
d) Biểu đồ tần số
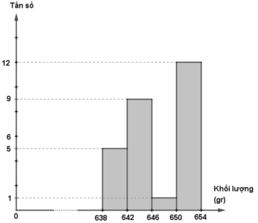
- Đường gấp khúc tần số
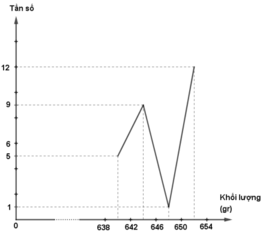
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
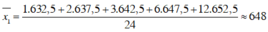
- Phương sai:
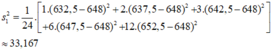
- Độ lệch chuẩn:
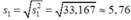
* Xét bảng phân bố ở câu b):
- Số trung bình:
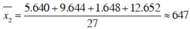
- Phương sai:
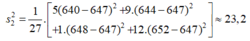
- Độ lệch chuẩn:
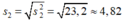
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.
Xét bảng phân bố tần số và tần suất ghép lớp đã được lập ở bài tập số 3 của bài 1.
a) Hãy vẽ biểu đồ tần suất hình cột, đường gấp khúc tần suất.
b) Hãy vẽ biểu đồ tần số hình cột, đường gấp khúc tần số.
c) Dựa vào biểu đồ tần suất hình cột đã vẽ ở câu a, hãy nêu nhận xét về khối lượng của 30 củ khoai tây được khảo sát.
| Lớp của khối lượng | Tần số | Tần suất |
| [70; 80) | 3 | 10% |
| [80; 90) | 6 | 20% |
| [90; 100) | 12 | 40% |
| [100; 110) | 6 | 20% |
| [110; 120) | 3 | 10% |
| Cộng | 30 | 100% |
a) Biểu đồ tần suất hình cột:
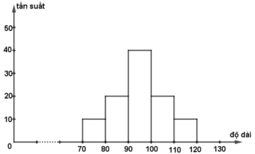
Biểu đồ tần suất hình gấp khúc:
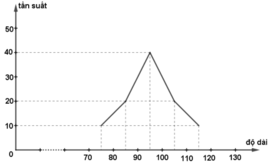
b) Biểu đồ tần số hình cột:
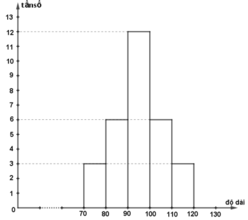
Biểu đồ tần số đường gấp khúc:
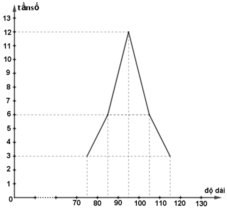
c) Dựa vào biểu đồ tần suất hình cột ta nhận thấy khối lương khoai tây thường nằm trong khoảng từ 90 đến 100 gram.
Cho các số liệu thống kê được ghi trong hai bảng sau đây :
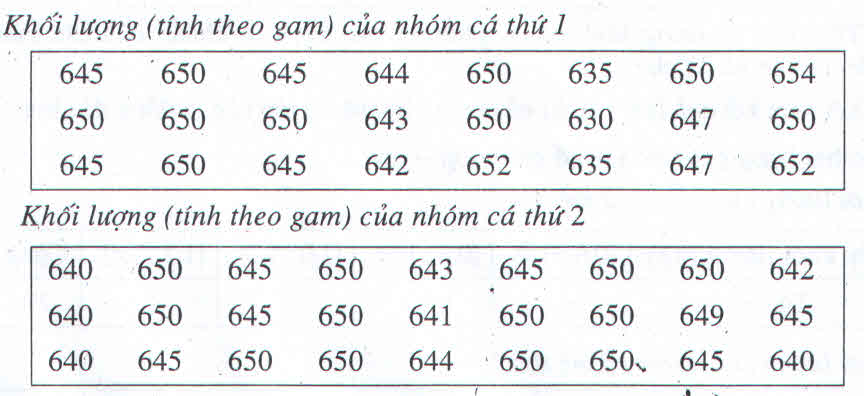
a. Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 1 với các lớp là :
[630;635); [635;640); [640;645); [645;650); [650;655]
b. Lập bảng phân bố tần số và tần suất ghép lớp theo nhóm cá thứ 2 với các lớp là :
[638;642); [642;646); [646;650); [650;654]
c. Mô tả bảng phân bố tần suất ghép lớp đã được lập ở câu a) bằng cách vẽ biểu đồ tần suất hình cột và đường gấp khúc tần suất ?
d. Mô tả bảng phân bố tần số ghép lớp đã được lập ở câu b), bằng cách vẽ biểu đồ tần số hình cột và đường gấp khúc tần số
e. Tính số trung bình cộng, phương sai và độ lệch chuẩn của các bảng phân bố tần số và tần suất ghép lớp đã lập được
Từ đó, xem xét nhóm cá nào có khối lượng đồng đều hơn ?
a) Bảng phân bố tần số và tần suất:
b) Bảng phân bố tần số và tần suất:
c) Biểu đồ tần suất hình cột:
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) Xét bảng phân bố ở câu a)
- Số trung bình cộng:
Từ đó ta thấy nhóm cá thứ 2 có khối lượng đồng đều hơn.
Cho bảng phân bố tần số ghép lớp sau
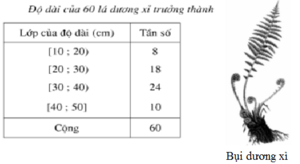
a) Lập bảng phân bố tần suất ghép lớp.
b) Dựa vào kết quả câu a, hãy nêu rõ trong 60 lá dương xỉ được khảo sát:
Số lá có chiều dài 30 cm chiếm bao nhiêu phần trăm?
Số lá có chiều dài từ 30 cm đến 50 cm chiếm bao nhiêu phần trăm?
a) Bảng phân bố tần suất ghép lớp:
| Lớp của chiều dài (cm) | Tần suất |
|---|---|
| [10; 20) | 13,3 |
| [20; 30) | 30,0 |
| [30; 40) | 40,0 |
| [40; 50) | 16,7 |
| Cộng | 100 (%) |
b) Tỉ lệ lá có chiều dài dưới 30 cm là:
13,3 + 30 = 43,3 %
Tỉ lệ lá có chiều dài từ 30 cm đến 50 cm là:
40 + 16,7 = 56,7 %
a) Mô tả bảng phân bố tần số ghép lớp đã lập được ở bài tập số 3, bằng cách vẽ biểu đồ tần số hình cột; vẽ đường gấp khúc tần số
b) Mô tả bảng phân bố tần suất ghép lớp đã lập được ở bài tập số 3 bằng cách vẽ biểu đồ tần suất hình cột; vẽ đường gấp khúc tần suất
c) Dựa vào biểu đồ tần suất hình cột đã vẽ được ở câu b), nêu nhận xét về thời gian đi từ nhà đến trường của bạn A trong 35 ngày được khảo sát ?


c) Trong 35 ngày đến trường của bạn A, ta thấy :
- Chiếm tỉ lệ thấp nhất (11,43%) là những ngày bạn A có thời gian đến trường từ 27 phút đến 29 phút (ứng với cột thấp nhất của biểu đồ)
- Chiếm tỉ lệ cao nhất (28,57%) là những ngày bạn A có thời gian đến trường từ 23 phút đến dưới 25 phút (ứng với cột cao nhất của biểu đồ)
- Đa số các ngày (74,28%), bạn A có thời gian đến trường từ 21 phút đến dưới 27 phút (ứng với 3 cột cao trội lên của biểu đồ)