Chứng minh rằng S ≤ a 2 + b 2 4 với S là diện tích của tam giác có độ dài hai cạnh là a,b ?

Những câu hỏi liên quan
Chứng minh rằng : a) S \(\le\frac{a^2+b^2}{4}\)với S là diện tích của tam giác có độ dài hai cạnh bằng a , b .
S = a.b/2
Xét : a^2+b^2/4 - ab/2 = a^2+b^2-2ab/4 = (a-b)^2/4 >= 0
=> ab/2 < = a^2+b^2/4
=> S < = a^2+b^2/4
=> đpcm
Tk mk nha
Đúng 0
Bình luận (0)
Bạn dưới Nguyễn Anh Quân nhầm rồi ; đây là tam giác thường chứ ko phải tam giác vuông
Đúng 0
Bình luận (0)
Chứng minh:
a) S \(\le\) \(\frac{a^2+b^2}{4}\)với S là diện tích tam giác có độ dài 2 cạnh bằng a,b
b) S \(\le\) \(\frac{a^2+b^2+c^2+d^2}{4}\)với S là diện tích tứ giác có độ dài 4 cạnh bằng a, b, c, d
gọi S là diện tích tứ giác ABCD có độ dài các cạnh là a,b,c,d .
Chứng minh rằng : S ≤( a2+b2+c2+d2 )/4
Cho S là diện tích của tứ giác ABCD có độ dài các cạnh là a, b, c, d. Chứng minh S ≤ (a^2 + b^2 + c^2 + d^2)/4
Cho tam giác ABC với độ dài 3 cạnh là a,b,c và diện tích S. Chứng minh S ≤ 1 / 16 ( 3a^2 + 2 b^2 + 2 c^2 )
Cho tứ giác ABCD nội tiếp đường tròn (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD (
H
∈
A
B
;
K
∈
A
D
).a) Chứng minh tứ giác AHIK nội tiếp đường tròn. b) Chứng minh rằng IA.IC IB.ID.c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.d) Gọi S là diện tích tam giác ABD, S’ là diện tích tam giác HIK. Chứng minh rằng:
S
S
≤...
Đọc tiếp
Cho tứ giác ABCD nội tiếp đường tròn (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD ( H ∈ A B ; K ∈ A D ).
a) Chứng minh tứ giác AHIK nội tiếp đường tròn.
b) Chứng minh rằng IA.IC = IB.ID.
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
d) Gọi S là diện tích tam giác ABD, S’ là diện tích tam giác HIK. Chứng minh rằng: S ' S ≤ H K 2 4. A I 2
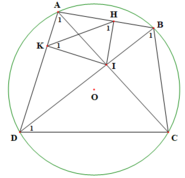
a) Tứ giác AHIK có:
A H I ^ = 90 0 ( I H ⊥ A B ) A K I ^ = 90 0 ( I K ⊥ A D ) ⇒ A H I ^ + A K I ^ = 180 0
=> Tứ giác AHIK nội tiếp.
b) ∆ IAD và ∆ IBC có:
A ^ 1 = B ^ 1 (2 góc nội tiếp cùng chắn cung DC của (O))
A I D ^ = B I C ^ (2 góc đối đỉnh)
=> ∆ IAD ~ ∆ IBC (g.g)
⇒ I A I B = I D I C ⇒ I A . I C = I B . I D
c, Xét đường tròn ngoại tiếp tứ giác AHIK có K ^ 1 = D ^ 1
A ^ 1 = H ^ 1 (2 góc nội tiếp cùng chắn cung IK)
mà A ^ 1 = B ^ 1 ⇒ H ^ 1 = B ^ 1
Chứng minh tương tự, ta được K ^ 1 = D ^ 1
∆ HIK và ∆ BCD có: H ^ 1 = B ^ 1 ; K ^ 1 = D ^ 1
=> ∆ HIK ~ ∆ BCD (g.g)
d) Gọi S1 là diện tích của ∆ BCD.
Vì ∆ HIK ~ ∆ BCD nên:
S ' S 1 = H K 2 B D 2 = H K 2 ( I B + I D ) 2 ≤ H K 2 4 I B . I D = H K 2 4 I A . I C (1)
Vẽ A E ⊥ B D , C F ⊥ B D ⇒ A E / / C F ⇒ C F A E = I C I A
∆ ABD và ∆ BCD có chung cạnh đáy BD nên:
S 1 S = C F A E ⇒ S 1 S = I C I A (2)
Từ (1) và (2) suy ra
S ' S 1 ⋅ S 1 S ≤ H K 2 4 I A . I C ⋅ I C I A ⇔ S ' S ≤ H K 2 4 I A 2 (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có diện tích S. Gọi S1 là diện tích hình tròn ngoại tiếp tam giác, S2 là diện tích hình tròn nội tiếp tam giác. Chứng minh rằng 2S < S1 + S2.
Cho hình vuông biết diện tích là 81cm vuông.Tính độ dài một cạnh.
Chời ơi bài này dễ thế mà đứa học sinh lớp 1 còn biết làm?
EM MÌNH LỚP 1 NHẮM MẮT CŨNG LÀM ĐƯỢC NỮA
Câu 4. ( 6,0 điểm ) Cho đường tròn tâm O bán kính R. Lấy một điểm S sao cho SO = 2R . Từ S kẻ các tiếp tuyến SA và SB với đường tròn ( A , B là các tiếp điểm ) .
a ) Chứng minh rằng tứ giác SAOB nội tiếp .
b ) Chứng minh rằng tam giác SAB là tam giác đều .
c ) Tính diện tích hình phẳng giới hạn bởi 2 tiếp tuyến SA , SB và cung nhỏ AB của đường tròn ( 0 )
với a,b,c là các cạhj của tam giác,S là diện tích ,P là nửa chu vi
Chứng minh S2=P.(P-a).(P-b).(P-c)














